Happy New Year: quantum computer emulator in SQL
Last year, my good friend and colleague Matt Ward challenged me to implement a quantum computer emulator in SQL.
Challenge accepted!
This year we will be building an SQL query which will emulate a quantum computer. This query will process quantum assembly, build the circuit, run the emulation and make the measurements.

First things first, a little bit of theory. I won't go deep into quantum mechanics now (primarily because I don't understand it well enough to talk about it in public). What we really need to know about emulating a quantum computer, is that it's all about matrix multiplication. Quantum computers run on physical effects which are hard to wrap one's head around, but relatively easy to express using quite simple math. This math is something you can work with, even if you don't understand the physics behind it on an intuitive level.
Theory
For this article, I will assume that you are familiar with the mathematics of matrix multiplication. If you're not, you'll need to read up a little bit on linear algebra. This is not a particularly hard topic, and it's being used heavily in many areas of programming: image processing, sound processing, quantitative finance analysis and many others. It is very rewarding to be familiar with it.
Qubits
So, quantum computers have registers (tiny blocks of memory), in pretty much the same way as the CPU in your laptop or phone does. The data stored in your CPU registers tells it what to do next, and these registers are being constantly updated as your CPU runs code.
Classic registers have bits, which store zeros and ones. These are exclusive: if the bit is on, it's not off, and if it's off, it's not on.
Quantum registers have qubits, which also store zeros and ones. But these zeros and ones are not exclusive. A qubit may be on, may be off, and may be somewhere in between. It's not like an on-off switch, but more like a computer trackball with a permanent marker dot on it. You can turn any way you like, and the dot position reflects the state of the qubit. The closer the dot is to the top (or to the bottom), the more "zero" or "one" the qubit is. The marked dot on the trackball can also turn about the vertical axis, which is also something that the qubit can store.
This is confusing, and you might need to read up on quantum mechanics to grasp it. But don't worry about it now. What we have to know about the qubit is that we need two complex numbers to describe it. The first number describes how much of "zero" it is, and the second one describes how much of "one" it is. These complex numbers' norms should add up to 1.
With classical registers, when we add another bit in the mix, we double the number of states the register can be in. So, a two-bit register has four possible states: 00, 01, 10, and 11. These states are mutually exclusive. If the register is 00, it cannot be 01 at the same time. This is why we are able to use two bits to describe the four states.
This does not work the same way with qubits. One qubit can be somewhat |0⟩ and somewhat |1⟩. Two qubits can be somewhat |00⟩, somewhat |01⟩, somewhat |10⟩, and somewhat |11⟩. To describe two qubits, we need four complex numbers. Their norms still have to add up to 1, but otherwise they can be any old numbers. This means that when two qubits are used together, they are not just two separate qubits anymore. It's possible that a two-qubits register is somewhat |00⟩, and somewhat |11⟩, but none of |01⟩ or |10⟩, all at the same time. It is, in a sense, larger than the sum of its parts. This is called entanglement. Three qubits can be in any mix of states from |000⟩ through |111⟩, which means 8 different complex numbers to describe every state's share in the mix. And so on. It is not enough to describe the state of every qubit in the register. We need two complex numbers to describe every combination of the qubits.
You might have wondered what these weird notations with the vertical var and the angle bracket mean. They are a part of Dirac's bra-ket notation. When I use it, it means I'm talking about these strange half this, half that qubit states, as opposed to straight and honest classical bits. But again, if you are not already familiar with all that, don't worry about it now. Many bright scientific minds have struggled with understanding this problem in depth.
For now, we just need to remember that if we have a register of N qubits, we need 2N complex numbers to describe its state.
As you can probably see now, this is where the problem of emulating quantum computers starts to show. A laptop or phone CPU these days probably has high tens or maybe low hundreds of 64-bit and 128-bit registers, so let's say something in the order of magnitude of 10000 bits of state. If we were to emulate a classical CPU using a computer program, we would need to have 10000 bits of memory to keep this state. These days, 10000 bits of memory is nothing.
But to emulate 10000 qubits, we would need to use about 210000 bits of memory. That's about 103000 bytes. It's hell of a lot of memory. If we take all the memory that has been and will ever be produced on the planet Earth, and plug it into our emulator, we will still be 103000 bytes short of our target goal.
In practice, a laptop can emulate 20-qubit or so quantum registers. Supercomputers can do high forties.
State evolution
When a CPU is running code, it looks into its registers and decides what to do next, using quite complicated logic. The CPU also usually has access to external devices (like RAM), and its control flow can be changed by external events like interrupts and exceptions.
The quantum flow is much dumber. A purely quantum algorithm does not have branches, external data, or any kind of control flow. It consists of a series of gates, one after another, each of them changing the state of the quantum register. There is relatively simple math behind those changes.
If we have a quantum register with N qubits, we can describe its state using 2N complex numbers. Each of these numbers can be completely independent of the others (again, as long as their norms add up to one), so we kind of need to store all of them. We store them in an array. Mathematically speaking, this array represents a normalized vector in 2N-dimensional complex space.
When we run the register through a quantum gate (or, as they put it, "evolve" the register), its state changes according to certain math rules. Each quantum gate is, in essence, a square 2N by 2N complex matrix. The old state of the register gets multiplied by the gate's matrix and becomes the new state.
Unitary matrices
The gates' matrices have to be unitary. This means that if we take its conjugate transpose (turn the matrix about the diagonal and change the signs of all the imaginary parts in every element) and multiply it by the original matrix, we'll get the identity matrix back. Identity means a matrix with all 1's in the diagonal cells and all 0's in all the other cells. Multiplying any vector by the identity matrix always gives the same vector back. This is why it's called identity.
Unitary matrices have two important properties.
First of all, if you multiply a vector by it, the result will have the same norm. This means that if the register state was normalized before the gate, it will remain normalized after.
Second, they are reversible. If you take another gate, whose matrix is the conjugate transpose of the original gate, and evolve the register through both of these gates, you will get the same exact state back. Can you see why? Remember that matrix multiplication is associative.
Unitary matrices let you get from any normalized vector to any other normalized vector and back.
So, in essence, all that quantum computing allows you to do is take a normalized vector with 2N complex elements and transform it to another normalized vector with 2N complex elements, according to some rules. That's all there is to it.
Turns out, that being able to do these transformations fast is a very good thing. An N-qubit register can in fact store 2N complex numbers and transforming this register through the unitary matrices is done by the same machinery that runs our universe, which is very fast. These transformations can sometimes be designed to do the same things as really important functions which would take very long to compute on a classical computer. To be able to make these transformations fast would be the same as to be able to compute these functions 2N times at once.
Every ideal quantum circuit will evolve the state in a deterministic way. If we run the same input state through the circuit, we will always get the same output state once all the evolutions are done. In this sense, a quantum circuit is not that much a program, as it is a function, which rotates (and possibly reflects) vectors about a constant axis in 2N-dimensional complex space. That's what all the fuss is about.
Come to think of it, a quantum computer is just a glorified circular slide rule — in 2N dimensions. Yet, it is immensely useful to have these kinds of transformations implemented in, so to say, hardware, because they do solve real-world problems and they are very hard to compute on classical computer.
Measurement
Once the quantum register has gone through all the evolutions, it gets into a new state. But here's the thing: we cannot read this state. The universe machinery that is doing the matrix multiplication so fast for us, unfortunately, does not allow to read its results. When we try to read a quantum register, the universe randomly selects a position in the array, and magically puts the number one into that position, and zeros on all the others. By trying to read a quantum register, we change its state, and there is no way around it. This phenomenon is called wave function collapse, which is another mystic thing you might have heard about.
There is still a way to retrieve at least some information about the final state. When we measure qubits, the probability to get a certain combination of 0's and 1's is equal to the norm of the complex number in the state which describes this combination. If we have a two-qubit register in this state: , then the probability of measuring every possible combinations of 0's and 1's is equal to 0.25 (which is the norm of the complex number 0.5). If the state looks like this:
, then the probability of measuring 00 or 11 is equal to 0.5, and the probabilities of measuring 01 or 10 are zero. But the measurement will return either 00 or 11, and there is no way of telling in advance which one it will be. And since the measurement of 00 would replace the state with
, all subsequent measurements of the register would return the same value of 00 (because it is the only one left with a non-zero probability amplitude).
The universe does not come equipped with a debugger. We cannot tap into the inner workings of quantum mechanics and see what is going on there. If we tried to do that, this would count as a measurement, and this would break the state (or "collapse" it).
We cannot look inside a quantum circuit. But something we can do is re-run the experiment multiple times. As we remember, a quantum circuit is a deterministic function. If we feed it the same input state, it will evolve it into the same output state every time. When we try to measure this state, it will collapse differently for each experiment. By looking at how often different combinations of 0's and 1's turn up in measurements, we can estimate what the coefficients in the original state vector were.
And this is exactly how we use the quantum computer:
- We use our math knowledge to build a set of gates that would turn the initial state vector into another state vector, which would somehow encode the answer that we need. The initial state vector usually has all the qubits initialized to |0⟩. This means that it has 1 for the state |000..0⟩, and 0's for all the other states
- The target state vector will be very large, and we will not be able to calculate all its values directly. But we will know that these values will be larger for certain states and smaller for the others, because this is how we arranged the gates
- On a hardware quantum device, we arrange the quantum gates, run the initial state through them many times, and make the measurements of each result
- From looking at the distribution of the measurement results, we estimate the norms of the components of the target vector. The distribution of frequencies of the register states turning up in measurements will encode the answer to our problem
Phases
The coefficients in the state vector (they are called probability amplitudes) are complex numbers. If a certain combination of 0's and 1's (each one of these combinations is called an eigenstate) has the probability amplitude of 0.5, this particular combination will show up in the measurements one time of four, on average. But the same would be true if the probability amplitude of this eigenstate were -0.5, or 0.5i, or -0.5i, or, in fact, any complex number whose norm is 0.25 (there are infinitely many of them). We cannot tell these probability amplitudes apart by looking at the measurements. The state vector does have them as complex numbers, and it does matter when the state evolves. It is called a "relative phase", or phase difference between probability amplitudes of different eigenstates. Relative phases have physical significance and do matter in register evolutions, but cannot be measured, statistically or otherwise. The final state cannot have the answer encoded in the relative phases of the probability amplitudes, because they are impossible to measure. The answer has to be encoded in the amplitudes' norms.
On the other hand, if you multiply the state vector by a complex number with the norm 1 (which means multiplying all its components by this number), this factor will remain in the state all the way through its evolution. This is easy to verify: the quantum circuit, ultimately, multiples the state vector by a matrix, and the scalar multiplication of vectors and matrices is associative. This is called a "global phase", because it acts on all the eigenstates in the same way. Unlike relative phases, the global phase does not have any physical significance. It does not affect evolutions in any meaningful way, and of course it cannot be measured experimentally. Register states which only differ in global phase, do not really differ at all, not in any way that we can detect.
A little digression. An astute reader might have noticed that earlier I was talking about encoding a single qubit as a position of a trackball with a dot on it. The position of a trackball can be encoded with two real numbers (elevation and azimuth angles), but the qubit state is described with two complex numbers. Turns out that if we disregard the global phase and take into account the fact that for a single qubit the amplitudes have to be normalized (their norms need to add up to 1), we can indeed encode these two complex numbers with two real ones. But this is only true for a single qubit. To describe two or more qubits, we will still need the complex vector space.
Gates
Now, what kind of gates (or matrices) can we use to build our quantum circuits?
Different types of quantum computers use different kinds of gates. The IBM Q family uses the U1(λ) gate, the RX(π/2) gate, and the CNOT gate. Here are their matrices:
The first two gates act on one qubit, the CNOT (otherwise called CX) acts on two.
If our quantum register has more qubits than the gate transforms (and any useful register does), we extend the matrix by Kronecker multiplying it with an identity matrix. Here's what the transformation matrix looks like for a three-qubit register with a CNOT gate on qubits 0 and 1:
Turns out that by combining (multiplying) these three basic transformations, you can build any unitary matrix.
Hardware implementation
All above works in theory. With the real hardware, there are some implementation problems:
- The qubits are very hard to build and maintain. IBM recently announced that they had developed a 127-qubit processor, which is the bleeding edge technology at the time of this writing
- Quantum machines are very sensitive to environment noise. They have to live in a deep freezer at mK temperatures and be shielded from any radiation, including radio waves. Any interaction with the outer world halfway through the experiment collapses the wave function and messes up the register state. This means that the measurement statistics will be off, possibly to the point where the peaks in probabilities for certain states drown in noise
- Theoretically, we can use gates to connect any pair of qubits in the register. In practice, qubits have connectivity diagrams. This means that you can apply the CNOT gates only between certain pairs of qubits, and only in certain directions. There are ways to overcome these limitations by stacking the gates in clever ways, but this makes circuits longer and more prone to noise.
Despite all these limitations, quantum computers do exist and work. IBM offers free access to them, and a really nice SDK to work with them called Qiskit. You can use it to design and build quantum circuits and run them on real quantum hardware in the cloud.
I hope I didn't make any blatant mistakes in my overview. With that out of the way, let's jump to the implementation.
Implementation in SQL
To test our simulator, we will implement a 2x2 binary Sudoku solver using Grover's algorithm. I adapted this algorithm straight from the Qiskit textbook.
Complex number helpers
To work with complex numbers, it would be really helpful to have complex types. PostgreSQL does not have a complex number type built-in, so I will create a type for complex numbers, as well as some functions to work with this type. Usually, I use pure SQL for my SQL magic posts, because using procedural code is cheating in kills the magic. But these types are just thin wrappers around some lengthy expressions, and the functions don't have any procedural code in them.
Here are the types I created:
DROP TYPE IF EXISTS COMPLEX CASCADE;
CREATE TYPE COMPLEX AS (r DOUBLE PRECISION, i DOUBLE PRECISION);
CREATE OR REPLACE FUNCTION complex(a DOUBLE PRECISION)
RETURNS complex
AS
$$
SELECT (a, 0)::COMPLEX;
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP CAST IF EXISTS (DOUBLE PRECISION AS COMPLEX);
CREATE CAST (DOUBLE PRECISION AS COMPLEX)
WITH FUNCTION complex(DOUBLE PRECISION);
CREATE OR REPLACE FUNCTION complex(a INT)
RETURNS complex
AS
$$
SELECT a::DOUBLE PRECISION::COMPLEX;
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP CAST IF EXISTS (INT AS COMPLEX);
CREATE CAST (INT AS COMPLEX)
WITH FUNCTION complex(INT);
CREATE OR REPLACE FUNCTION pos(a COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT a
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS + (NONE, complex);
CREATE OPERATOR +
(
RIGHTARG = complex,
PROCEDURE = pos
);
CREATE OR REPLACE FUNCTION neg(a COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT (-a.r, -a.i)::COMPLEX
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS - (NONE, complex);
CREATE OPERATOR -
(
RIGHTARG = complex,
PROCEDURE = neg
);
CREATE OR REPLACE FUNCTION add (a COMPLEX, b COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT (a.r + b.r, a.i + b.i)::COMPLEX
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS + (complex, complex);
CREATE OPERATOR +
(
LEFTARG = complex,
RIGHTARG = complex,
PROCEDURE = add,
COMMUTATOR = +
);
CREATE OR REPLACE FUNCTION mul (a COMPLEX, b COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT (a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r)::COMPLEX
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS * (complex, complex);
CREATE OPERATOR *
(
LEFTARG = complex,
RIGHTARG = complex,
PROCEDURE = mul,
COMMUTATOR = *
);
CREATE OR REPLACE FUNCTION mul (a COMPLEX, b DOUBLE PRECISION)
RETURNS COMPLEX
AS
$$
SELECT (a.r * b, a.i * b)::COMPLEX
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS * (complex, DOUBLE PRECISION);
CREATE OPERATOR *
(
LEFTARG = complex,
RIGHTARG = DOUBLE PRECISION,
PROCEDURE = mul,
COMMUTATOR = *
);
CREATE OR REPLACE FUNCTION mul (a DOUBLE PRECISION, b COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT b * a
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS * (DOUBLE PRECISION, COMPLEX);
CREATE OPERATOR *
(
LEFTARG = DOUBLE PRECISION,
RIGHTARG = COMPLEX,
PROCEDURE = mul,
COMMUTATOR = *
);
CREATE OR REPLACE FUNCTION norm(a COMPLEX)
RETURNS DOUBLE PRECISION
AS
$$
SELECT a.r * a.r + a.i * a.i
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
CREATE OR REPLACE FUNCTION magnitude(a COMPLEX)
RETURNS DOUBLE PRECISION
AS
$$
SELECT SQRT(norm(a))
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS ~ (NONE, complex);
CREATE OPERATOR ~
(
RIGHTARG = complex,
PROCEDURE = magnitude
);
CREATE OR REPLACE FUNCTION conjugate(a COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT (a.r, -a.i)::COMPLEX
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS # (NONE, complex);
CREATE OPERATOR #
(
RIGHTARG = complex,
PROCEDURE = conjugate
);
CREATE OR REPLACE FUNCTION div (a COMPLEX, b DOUBLE PRECISION)
RETURNS COMPLEX
AS
$$
SELECT (a.r / b, a.i / b);
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS / (complex, DOUBLE PRECISION);
CREATE OPERATOR /
(
LEFTARG = complex,
RIGHTARG = DOUBLE PRECISION,
PROCEDURE = div
);
CREATE OR REPLACE FUNCTION rec (a COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT #a / norm(a)
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS // (NONE, COMPLEX);
CREATE OPERATOR //
(
RIGHTARG = COMPLEX,
PROCEDURE = rec
);
CREATE OR REPLACE FUNCTION div (a COMPLEX, b COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT a * //b
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
DROP OPERATOR IF EXISTS / (COMPLEX, COMPLEX);
CREATE OPERATOR /
(
LEFTARG = COMPLEX,
RIGHTARG = COMPLEX,
PROCEDURE = div
);
CREATE OR REPLACE FUNCTION exp(a COMPLEX)
RETURNS COMPLEX
AS
$$
SELECT EXP(a.r) * (COS(a.i), SIN(a.i))::COMPLEX
$$
LANGUAGE 'sql'
IMMUTABLE
STRICT;
CREATE AGGREGATE SUM(COMPLEX)
(
STYPE = COMPLEX,
SFUNC = add
);
Gate definitions
For our quantum circuit, we need to define some gates. As I told before, there are just three gates that the IBM hardware is using under the hood, and you can build all other gates by combining these three. In the SDK, you can use more complex gates. The hardware which runs the circuit will figure out how to construct them from the building blocks.
We will be using the Pauli gates X, Y, and Z; the Hadamard gate H; and the multi-qubit controlled-NOT (generalized Toffoli) gates CnX, connecting from 2 to 5 qubits.
For the single-qubit gates, we will define the matrices explicitly; for the Toffoli, we will do it programmatically.
WITH gates (opcode, arity, matrix) AS MATERIALIZED
(
VALUES
('X', 1, ARRAY[
[0, 1],
[1, 0]
]::COMPLEX[][]),
('Y', 1, ARRAY[
[0, -(0, 1)],
[-(0, 1), 0]
]::COMPLEX[][]),
('Z', 1, ARRAY[
[1, 0],
[0, -1]
]::COMPLEX[][]),
('H', 1, ARRAY[
[1 / SQRT(2), 1 / SQRT(2)],
[1 / SQRT(2), -1 / SQRT(2)]
]::COMPLEX[][])
UNION ALL
SELECT REPEAT('C', arity - 1) || 'X', arity, matrix
FROM GENERATE_SERIES(2, 5) arity
CROSS JOIN LATERAL
(
WITH constants AS
(
SELECT (1 << (arity - 1)) - 1 AS mask,
(1 << arity) - 1 AS rank
)
SELECT ARRAY_AGG(cols ORDER BY row) AS matrix
FROM constants
CROSS JOIN LATERAL
(
SELECT row, ARRAY_AGG((CASE WHEN row & mask = mask AND col & mask = mask THEN row <> col ELSE row = col END)::INT::COMPLEX ORDER BY col) cols
FROM GENERATE_SERIES(0, rank) row
CROSS JOIN
GENERATE_SERIES(0, rank) col
GROUP BY
row
) gate
) toffoli
)
SELECT opcode, arity,
(
SELECT STRING_AGG(cols::TEXT, E'\n' ORDER BY row)
FROM (
SELECT row, ARRAY_AGG(coefficient ORDER BY col) cols
FROM (
SELECT (r, i)::COMPLEX coefficient,
(ordinality - 1) / (1 << arity) AS row, (ordinality -1 ) % (1 << arity) AS col
FROM UNNEST(matrix) WITH ORDINALITY matrix (r, i, ordinality)
) q
GROUP BY
row
) q
) matrix
FROM gates;
| opcode | arity | matrix |
|---|---|---|
| X | 1 | {"(0,0)","(1,0)"} {"(1,0)","(0,0)"} |
| Y | 1 | {"(0,0)","(-0,-1)"} {"(-0,-1)","(0,0)"} |
| Z | 1 | {"(1,0)","(0,0)"} {"(0,0)","(-1,0)"} |
| H | 1 | {"(0.7071067811865475,0)","(0.7071067811865475,0)"} {"(0.7071067811865475,0)","(-0.7071067811865475,0)"} |
| CX | 2 | {"(1,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(1,0)"} {"(0,0)","(0,0)","(1,0)","(0,0)"} {"(0,0)","(1,0)","(0,0)","(0,0)"} |
| CCX | 3 | {"(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)"} |
| CCCX | 4 | {"(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} |
| CCCCX | 5 | {"(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)"} {"(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(1,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)","(0,0)"} |
As you can see, the more qubits are in the gate, the larger the matrix is. Fortunately, most of the coefficients in the matrices that we are going to use are zeros. This will help us with the performance when we get there.
Assembly language
Now that we have the gates, we can build the circuit. We will encode it in a text string, using assembly language of my own invention. The grammar is dirt simple: semicolon-separated gates, colon-separated opcodes, and comma-separated inputs. Whitespaces and line breaks to taste.
WITH RECURSIVE
settings AS
(
SELECT 9 AS qubits,
ARRAY[0, 1, 2, 3] AS measurements,
'
H: 8;
Z: 8;
H: 0;
H: 1;
H: 2;
H: 3;
CX: 0,4;
CX: 1,4;
CX: 0,5;
CX: 2,5;
CX: 1,6;
CX: 3,6;
CX: 2,7;
CX: 3,7;
CCCCX: 4,5,6,7,8;
CX: 0,4;
CX: 1,4;
CX: 0,5;
CX: 2,5;
CX: 1,6;
CX: 3,6;
CX: 2,7;
CX: 3,7;
H: 0;
H: 1;
H: 2;
H: 3;
X: 0;
X: 1;
X: 2;
X: 3;
H: 3;
CCCX: 0,1,2,3;
H: 3;
X: 0;
X: 1;
X: 2;
X: 3;
H: 0;
H: 1;
H: 2;
H: 3;
CX: 0,4;
CX: 1,4;
CX: 0,5;
CX: 2,5;
CX: 1,6;
CX: 3,6;
CX: 2,7;
CX: 3,7;
CCCCX: 4,5,6,7,8;
CX: 0,4;
CX: 1,4;
CX: 0,5;
CX: 2,5;
CX: 1,6;
CX: 3,6;
CX: 2,7;
CX: 3,7;
H: 0;
H: 1;
H: 2;
H: 3;
X: 0;
X: 1;
X: 2;
X: 3;
H: 3;
CCCX: 0,1,2,3;
H: 3;
X: 0;
X: 1;
X: 2;
X: 3;
H: 0;
H: 1;
H: 2;
H: 3;
' AS program
),
circuit AS MATERIALIZED
(
SELECT step, parts[1] AS opcode, inputs::INT[]
FROM settings
CROSS JOIN
REGEXP_SPLIT_TO_TABLE(program, E'\\s*;\\s*') WITH ORDINALITY instructions(instruction, step)
CROSS JOIN LATERAL
REGEXP_MATCHES(instruction, E'(\\w+)\\s*:\\s(.*)') parts
CROSS JOIN LATERAL
REGEXP_SPLIT_TO_ARRAY(parts[2], E'\\s*,\\s*') inputs
)
SELECT *
FROM circuit
ORDER BY
step
LIMIT 10
| step | opcode | inputs |
|---|---|---|
| 1 | H | [8] |
| 2 | Z | [8] |
| 3 | H | [0] |
| 4 | H | [1] |
| 5 | H | [2] |
| 6 | H | [3] |
| 7 | CX | [0, 4] |
| 8 | CX | [1, 4] |
| 9 | CX | [0, 5] |
| 10 | CX | [2, 5] |
Global unitary matrices from state matrices
To evolve the state, we need to build the complete 2N×2N unitary matrix for each step. To do this, we will need to Kronecker multiply the identity matrix (for the non-input qubits) by the gate matrix (for the input qubits). We will return the resulting matrix as a rowset with row numbers, column numbers, and only non-zero coefficients in it.
For the Kronecker multiplication, we will use a little optimization trick. Because the identity matrix has zeros in non-diagonal elements, we can be sure that in the resulting matrix, the non-zero elements will only be in the rows and columns where the eigenstates of non-input qubits are the same.
Ok, this might be a little bit hard to parse. Here's an example.
Our circuit has 9 qubits. Let's assume we have a CX gate between inputs 0 and 1. The total unitary matrix for this gate will be a Kronecker product of the identity matrix for the qubits 2 through 9 (27×27 = 128×128), and the 4×4 CX matrix for the qubits 0 and 1.
In a transformation matrix, every row and every column corresponds to some eigenstate of the state vector. There is a row for the state |000000000⟩, a row for the state |000000001⟩, and so on. Similarly, there is a column for the state |000000000⟩, a column for the state |000000001⟩, and so on.
We can make a quick optimization when filling up the cells. We can look at the seven leftmost bits in the row's eigenstate and compare them to the seven leftmost bits in the column's eigenstate. If they are not equal, they will have a zero in the identity matrix. It means we should not be worrying about them at all, we can just skip them when building the query.
Only if the leftmost seven bits for the row and the column are equal, there is a change of having a non-zero value in the matrix.
This trick reduces the number of calculations from 4N to 2N for every matrix — in our case, by the factor of 512.
To calculate the resulting matrix, we will need to map it to the actual inputs used in the circuit, and then cross join it with the eigenstates of non-input qubits.
Let's see what the matrix looks like for the gate CCCCX between the inputs 0, 1, 2, 3 and 4.
WITH settings AS
(
SELECT 9 AS qubits
),
gates (opcode, arity, matrix) AS MATERIALIZED
(
VALUES
('X', 1, ARRAY[
[0, 1],
[1, 0]
]::COMPLEX[][]),
('Y', 1, ARRAY[
[0, -(0, 1)],
[-(0, 1), 0]
]::COMPLEX[][]),
('Z', 1, ARRAY[
[1, 0],
[0, -1]
]::COMPLEX[][]),
('H', 1, ARRAY[
[1 / SQRT(2), 1 / SQRT(2)],
[1 / SQRT(2), -1 / SQRT(2)]
]::COMPLEX[][])
UNION ALL
SELECT REPEAT('C', arity - 1) || 'X', arity, matrix
FROM GENERATE_SERIES(2, 5) arity
CROSS JOIN LATERAL
(
WITH constants AS
(
SELECT (1 << (arity - 1)) - 1 AS mask,
(1 << arity) - 1 AS rank
)
SELECT ARRAY_AGG(cols ORDER BY row) AS matrix
FROM constants
CROSS JOIN LATERAL
(
SELECT row, ARRAY_AGG((CASE WHEN row & mask = mask AND col & mask = mask THEN row <> col ELSE row = col END)::INT::COMPLEX ORDER BY col) cols
FROM GENERATE_SERIES(0, rank) row
CROSS JOIN
GENERATE_SERIES(0, rank) col
GROUP BY
row
) gate
) toffoli
),
gate AS MATERIALIZED
(
SELECT arity, matrix, ARRAY[0, 1, 2, 3, 4] AS inputs
FROM gates
WHERE gates.opcode = 'CCCCX'
),
identity_qubits AS MATERIALIZED
(
SELECT ARRAY_AGG(input ORDER BY input) identity_qubits
FROM settings
CROSS JOIN
gate
CROSS JOIN LATERAL
(
SELECT input
FROM GENERATE_SERIES(0, qubits - 1) input
EXCEPT
SELECT input
FROM UNNEST(inputs) input
) q
),
unitary AS
(
SELECT row, col, coefficient
FROM settings
CROSS JOIN
gate
CROSS JOIN LATERAL
(
SELECT circuit_identity_basis | circuit_gate_row_basis AS row,
circuit_identity_basis | circuit_gate_col_basis AS col,
coefficient
FROM gate
CROSS JOIN
identity_qubits
CROSS JOIN LATERAL
(
WITH circuit_gate_basis AS
(
SELECT gate_basis, circuit_gate_basis
FROM GENERATE_SERIES(0, (1 << arity) - 1) gate_basis
CROSS JOIN LATERAL
(
SELECT COALESCE(BIT_OR(1 << inputs[input + 1]), 0) AS circuit_gate_basis
FROM GENERATE_SERIES(0, arity - 1) input
WHERE gate_basis & (1 << input) > 0
) circuit_gate_basis
)
SELECT row.circuit_gate_basis AS circuit_gate_row_basis,
col.circuit_gate_basis AS circuit_gate_col_basis,
matrix[row.gate_basis + 1][col.gate_basis + 1]::COMPLEX AS coefficient
FROM circuit_gate_basis row
CROSS JOIN
circuit_gate_basis col
) circuit_gate_basis
CROSS JOIN LATERAL
(
SELECT circuit_identity_basis
FROM GENERATE_SERIES(0, (1 << (qubits - arity)) - 1) identity_basis
CROSS JOIN LATERAL
(
SELECT COALESCE(BIT_OR(1 << identity_qubit), 0) AS circuit_identity_basis
FROM UNNEST(identity_qubits) WITH ORDINALITY AS identity_qubits (identity_qubit, input)
WHERE identity_basis & (1 << (input - 1)::INT) > 0
) circuit_identity_basis
) circuit_identity_basis
) unitary
WHERE coefficient <> 0::COMPLEX
)
SELECT *
FROM unitary
ORDER BY
row, col, coefficient
| row | col | coefficient |
|---|---|---|
| 0 | 0 | (1,0) |
| 1 | 1 | (1,0) |
| 2 | 2 | (1,0) |
| 3 | 3 | (1,0) |
| 4 | 4 | (1,0) |
| 5 | 5 | (1,0) |
| 6 | 6 | (1,0) |
| 505 | 505 | (1,0) |
| 506 | 506 | (1,0) |
| 507 | 507 | (1,0) |
| 508 | 508 | (1,0) |
| 509 | 509 | (1,0) |
| 510 | 510 | (1,0) |
| 511 | 495 | (1,0) |
State evolution
To evolve the state of the register, we need to unnest its array, multiply it by the gate matrix and aggregate it back into the array. Matrix multiplication works very smoothly with SQL and translates quite naturally into joins, sums and group-by clauses.
There is a little problem with unnesting arrays of record types in PostgreSQL. The function UNNEST splits the record types into individual fieds. In the output of UNNEST there will be separate double precision fields for the real and the imaginary parts of the number. We will need to combine them back into the COMPLEX type.
Let us see how a single Hadamard gate acts on the register in the initial state (1 for the eigenstate |000000000⟩, 0 for all others):
WITH RECURSIVE
settings AS
(
SELECT 9 AS qubits
),
basis AS
(
SELECT eigenstate
FROM settings
CROSS JOIN
generate_series(0, (1 << qubits) - 1) AS eigenstate
),
gates (opcode, arity, matrix) AS MATERIALIZED
(
VALUES
('X', 1, ARRAY[
[0, 1],
[1, 0]
]::COMPLEX[][]),
('Y', 1, ARRAY[
[0, -(0, 1)],
[-(0, 1), 0]
]::COMPLEX[][]),
('Z', 1, ARRAY[
[1, 0],
[0, -1]
]::COMPLEX[][]),
('H', 1, ARRAY[
[1 / SQRT(2), 1 / SQRT(2)],
[1 / SQRT(2), -1 / SQRT(2)]
]::COMPLEX[][])
UNION ALL
SELECT REPEAT('C', arity - 1) || 'X', arity, matrix
FROM GENERATE_SERIES(2, 5) arity
CROSS JOIN LATERAL
(
WITH constants AS
(
SELECT (1 << (arity - 1)) - 1 AS mask,
(1 << arity) - 1 AS rank
)
SELECT ARRAY_AGG(cols ORDER BY row) AS matrix
FROM constants
CROSS JOIN LATERAL
(
SELECT row, ARRAY_AGG((CASE WHEN row & mask = mask AND col & mask = mask THEN row <> col ELSE row = col END)::INT::COMPLEX ORDER BY col) cols
FROM GENERATE_SERIES(0, rank) row
CROSS JOIN
GENERATE_SERIES(0, rank) col
GROUP BY
row
) gate
) toffoli
),
initial_state AS
(
SELECT ARRAY_AGG((CASE eigenstate WHEN 0 THEN 1 ELSE 0 END)::COMPLEX ORDER BY eigenstate) AS state
FROM basis
),
new_state AS
(
SELECT new_state.state
FROM settings
CROSS JOIN
initial_state
CROSS JOIN LATERAL
(
WITH gate AS MATERIALIZED
(
SELECT arity, matrix, ARRAY[0] AS inputs
FROM gates
WHERE gates.opcode = 'H'
),
identity_qubits AS MATERIALIZED
(
SELECT ARRAY_AGG(input ORDER BY input) identity_qubits
FROM gate
CROSS JOIN LATERAL
(
SELECT input
FROM GENERATE_SERIES(0, qubits - 1) input
EXCEPT
SELECT input
FROM UNNEST(inputs) input
) q
),
unitary AS
(
SELECT circuit_identity_basis | circuit_gate_row_basis AS row,
circuit_identity_basis | circuit_gate_col_basis AS col,
coefficient
FROM gate
CROSS JOIN
identity_qubits
CROSS JOIN LATERAL
(
WITH circuit_gate_basis AS
(
SELECT gate_basis, circuit_gate_basis
FROM GENERATE_SERIES(0, (1 << arity) - 1) gate_basis
CROSS JOIN LATERAL
(
SELECT COALESCE(BIT_OR(1 << inputs[input + 1]), 0) AS circuit_gate_basis
FROM GENERATE_SERIES(0, arity - 1) input
WHERE gate_basis & (1 << input) > 0
) circuit_gate_basis
)
SELECT row.circuit_gate_basis AS circuit_gate_row_basis,
col.circuit_gate_basis AS circuit_gate_col_basis,
matrix[row.gate_basis + 1][col.gate_basis + 1]::COMPLEX AS coefficient
FROM circuit_gate_basis row
CROSS JOIN
circuit_gate_basis col
) circuit_gate_basis
CROSS JOIN LATERAL
(
SELECT circuit_identity_basis
FROM GENERATE_SERIES(0, (1 << (qubits - arity)) - 1) identity_basis
CROSS JOIN LATERAL
(
SELECT COALESCE(BIT_OR(1 << identity_qubit), 0) AS circuit_identity_basis
FROM UNNEST(identity_qubits) WITH ORDINALITY AS identity_qubits (identity_qubit, input)
WHERE identity_basis & (1 << (input - 1)::INT) > 0
) circuit_identity_basis
) circuit_identity_basis
WHERE coefficient <> 0::COMPLEX
),
state AS
(
WITH state AS
(
SELECT (r, i)::COMPLEX amplitude, ordinality - 1 AS eigenstate
FROM UNNEST(state) WITH ORDINALITY state (r, i, ordinality)
)
SELECT row, SUM(amplitude * coefficient) AS amplitude
FROM state
JOIN unitary
ON col = eigenstate
GROUP BY
row
)
SELECT ARRAY_AGG(amplitude ORDER BY row) state
FROM state
) new_state
)
SELECT RIGHT((ordinality - 1)::BIT(9)::TEXT, qubits) eigenstate,
(r, i)::COMPLEX AS amplitude
FROM settings
CROSS JOIN
new_state
CROSS JOIN LATERAL
UNNEST(state) WITH ORDINALITY state(r, i, ordinality)
| eigenstate | amplitude |
|---|---|
| 000000000 | (0.7071067811865475,0) |
| 000000001 | (0.7071067811865475,0) |
| 000000010 | (0,0) |
| 000000011 | (0,0) |
| 000000100 | (0,0) |
| 111111011 | (0,0) |
| 111111100 | (0,0) |
| 111111101 | (0,0) |
| 111111110 | (0,0) |
| 111111111 | (0,0) |
The Hadamard gate puts the qubit 0 into a superposition of the states |0⟩ and |1⟩ with equal amplitudes. When we do the measurement, we will get 0 or 1 in the first qubit with equal probability. All the other qubits will always measure as 0.
Let us do a simulation of measurements of this register. For illustration purposes, we won't be bothering with emulating random experiments. Instead, we will calculate the theoretical probabilities. We will be measuring all qubits. For each state, we will just take the norm of its probability amplitude. This will be the probability to measure a register in this state.
WITH RECURSIVE
settings AS
(
SELECT 9 AS qubits,
ARRAY[0, 1, 2, 3, 4, 5, 6, 7, 8] AS measurements
),
basis AS
(
SELECT eigenstate
FROM settings
CROSS JOIN
generate_series(0, (1 << qubits) - 1) AS eigenstate
),
gates (opcode, arity, matrix) AS MATERIALIZED
(
VALUES
('X', 1, ARRAY[
[0, 1],
[1, 0]
]::COMPLEX[][]),
('Y', 1, ARRAY[
[0, -(0, 1)],
[-(0, 1), 0]
]::COMPLEX[][]),
('Z', 1, ARRAY[
[1, 0],
[0, -1]
]::COMPLEX[][]),
('H', 1, ARRAY[
[1 / SQRT(2), 1 / SQRT(2)],
[1 / SQRT(2), -1 / SQRT(2)]
]::COMPLEX[][])
UNION ALL
SELECT REPEAT('C', arity - 1) || 'X', arity, matrix
FROM GENERATE_SERIES(2, 5) arity
CROSS JOIN LATERAL
(
WITH constants AS
(
SELECT (1 << (arity - 1)) - 1 AS mask,
(1 << arity) - 1 AS rank
)
SELECT ARRAY_AGG(cols ORDER BY row) AS matrix
FROM constants
CROSS JOIN LATERAL
(
SELECT row, ARRAY_AGG((CASE WHEN row & mask = mask AND col & mask = mask THEN row <> col ELSE row = col END)::INT::COMPLEX ORDER BY col) cols
FROM GENERATE_SERIES(0, rank) row
CROSS JOIN
GENERATE_SERIES(0, rank) col
GROUP BY
row
) gate
) toffoli
),
initial_state AS
(
SELECT ARRAY_AGG((CASE eigenstate WHEN 0 THEN 1 ELSE 0 END)::COMPLEX ORDER BY eigenstate) AS state
FROM basis
),
new_state AS
(
SELECT new_state.state
FROM settings
CROSS JOIN
initial_state
CROSS JOIN LATERAL
(
WITH gate AS MATERIALIZED
(
SELECT arity, matrix, ARRAY[0] AS inputs
FROM gates
WHERE gates.opcode = 'H'
),
identity_qubits AS MATERIALIZED
(
SELECT ARRAY_AGG(input ORDER BY input) identity_qubits
FROM gate
CROSS JOIN LATERAL
(
SELECT input
FROM GENERATE_SERIES(0, qubits - 1) input
EXCEPT
SELECT input
FROM UNNEST(inputs) input
) q
),
unitary AS
(
SELECT circuit_identity_basis | circuit_gate_row_basis AS row,
circuit_identity_basis | circuit_gate_col_basis AS col,
coefficient
FROM gate
CROSS JOIN
identity_qubits
CROSS JOIN LATERAL
(
WITH circuit_gate_basis AS
(
SELECT gate_basis, circuit_gate_basis
FROM GENERATE_SERIES(0, (1 << arity) - 1) gate_basis
CROSS JOIN LATERAL
(
SELECT COALESCE(BIT_OR(1 << inputs[input + 1]), 0) AS circuit_gate_basis
FROM GENERATE_SERIES(0, arity - 1) input
WHERE gate_basis & (1 << input) > 0
) circuit_gate_basis
)
SELECT row.circuit_gate_basis AS circuit_gate_row_basis,
col.circuit_gate_basis AS circuit_gate_col_basis,
matrix[row.gate_basis + 1][col.gate_basis + 1]::COMPLEX AS coefficient
FROM circuit_gate_basis row
CROSS JOIN
circuit_gate_basis col
) circuit_gate_basis
CROSS JOIN LATERAL
(
SELECT circuit_identity_basis
FROM GENERATE_SERIES(0, (1 << (qubits - arity)) - 1) identity_basis
CROSS JOIN LATERAL
(
SELECT COALESCE(BIT_OR(1 << identity_qubit), 0) AS circuit_identity_basis
FROM UNNEST(identity_qubits) WITH ORDINALITY AS identity_qubits (identity_qubit, input)
WHERE identity_basis & (1 << (input - 1)::INT) > 0
) circuit_identity_basis
) circuit_identity_basis
WHERE coefficient <> 0::COMPLEX
),
state AS
(
WITH state AS
(
SELECT (r, i)::COMPLEX amplitude, ordinality - 1 AS eigenstate
FROM UNNEST(state) WITH ORDINALITY state (r, i, ordinality)
)
SELECT row, SUM(amplitude * coefficient) AS amplitude
FROM state
JOIN unitary
ON col = eigenstate
GROUP BY
row
)
SELECT ARRAY_AGG(amplitude ORDER BY row) state
FROM state
) new_state
)
SELECT eigenstate_bits, probability
FROM new_state
CROSS JOIN
settings
CROSS JOIN LATERAL
(
WITH probabilities AS
(
SELECT norm((r, i)::COMPLEX) AS probability, ordinality - 1 AS eigenstate
FROM UNNEST(state) WITH ORDINALITY state(r, i, ordinality)
)
SELECT RIGHT(measurement_eigenstate::BIT(36)::TEXT, ARRAY_LENGTH(measurements, 1)) AS eigenstate_bits,
SUM(probability)::NUMERIC(4, 4) AS probability
FROM probabilities
CROSS JOIN LATERAL
(
SELECT BIT_OR(((eigenstate >> qubit) & 1) << position::INT - 1) AS measurement_eigenstate
FROM UNNEST(measurements) WITH ORDINALITY measurements (qubit, position)
) measurement
GROUP BY
measurement_eigenstate
) measurements
WHERE probability >= 0.0001
ORDER BY
probability DESC, eigenstate_bits
| eigenstate_bits | probability |
|---|---|
| 000000000 | 0.5000 |
| 000000001 | 0.5000 |
Now we have all the machinery in place to run our simulation. Let's run an actual circuit!
We will run the algorithm to solve a binary 2×2 Sudoku puzzle. Each row and each column in a 2×2 square should have exactly one 1 and exactly one 0.
Here's the principle behind the Grover's algorithm.
Let's say we have a boolean-valued function which takes N-bit values and gives either 1 or 0 for every one of them. We need to find the values which give the 1 (or, maybe, just one value).
It might seem trivial — we know the function, we know the values, so all we need to do to apply the function for each value and see what it gives us. However, to know all the answers, we would need to apply this function 2N times. If the value of N is sufficiently large, it will take significant time to run all these repetitions.
This is what Bitcoin miners do all day long. Every Bitcoin transaction header has an empty slot to fill with 0's and 1's in such a way that its (double) SHA-256 hash be lower than a certain threshold. Even though the SHA-256 algorithm is relatively simple and there exist specialized circuits that can apply the hash billions of times per second, it still takes a significant amount of time and electricity to find a good value to put into this slot.
Another example of such a function would be factorization of a product of two sufficiently large primes. It would return 1 if the input is a factor of the product, 0 otherwise. Even though integer division is a relatively simple operation for a modern computer, it is still considered an impossible task to factorize a big enough number, because the number of repetition would be too large. A major part of modern cryptography is based on this assumption.
For some of these functions, we can design a quantum circuit which emulates calling this function. This circuit should flip the relative phase for the eigenstates which are the answers for the functions. Such a circuit is called "quantum oracle".
We cannot measure the relative phase of an eigenstate directly, but there's a circuit which allows to "amplify" the phases. After its application, the eigenstates with the phase flipped get an amplitude with a higher norm (and the rest of the states, of course, get an amplitude with a lower norm). These states get a higher chance to be measured.
It is trivial to code up such a function if we know its solutions. But the whole point of quantum algorithms is to find these solutions in the first place. So we need to tell the quantum algoritm the conditions of the function and let it come up with the answers. How exactly we do this (and if it's possible to do it at all), depends on the function. This is the trickest part of quantum programming.
So, for our Sudoku puzzle we need to do the following:
- Encode all possible solutions to the Sudoku puzzle as qubit eigenstates. There are 24 = 16 possible solutions, which can be encoded with 4 qubits
- Create a quantum oracle. It's a circuit which would flip the phase for the states that satisfy the Sudoku condition and leave it intact for those that don't.
- The Sudoku condition is "exactly one bit is set in each row and each column". It can be encoded by applying two CNOT gates for every rows and every columns, and having them control the "row and column" qubits.
- The qubit is reversed only if exactly one of two control inputs is 1 and other one is 0 in a row or column.
- All the row-and-column qubits control the "Sudoku" qubit through a four-way Toffoli gate.
- The Sudoku qubit is reversed only if all the conditions hold.
- By placing a Z gate on the "Sudoku" qubit, we introduce a phase difference between its |0⟩ and |1⟩ states. We do it to use a trick known as "phase kickback". The control qubit of a CNOT gate causes the target qubit to trigger (switch the amplitudes of |0⟩ and |1⟩ states of the target qubit). But this operation can also have effect on the control qubit. If there was a phase difference between the amplitudes of |0⟩ and |1⟩ states of the target qubit, this phase difference will propagate back to the control qubit after the evolution through the CNOT gate. This is exactly what we want to do: flip the phase on the eigenstates of the control qubits which have a component triggering the Sudoku qubit
- We need to uncompute the "cell" qubits and return them into the original eigenstate of |0000⟩. This is done by re-applying the CNOT gates. This will also propagate the phase kickback back to the original 4 qubits in the oracle
As we can see, the quantum oracle circuit requires more qubits to check all these conditions: 2 for rows, 2 for columns and 1 more for the total condition. These qubits are called the ancilla qubits. In classical computations, we could use the extra bits of memory as a scratchpad and dump them after we are done. But the quantum computation is reversible, so it's impossible to just ignore the ancilla bits. They are not going anywhere, and if they end up entangled with the oracle qubits, they will continue to influence them. This is why we need to bring the state of the ancilla bits back to the original eigenstate (or any other pure state)
- Apply the phase amplifier circuit to convert the relative phases into amplitudes with bigger norms
- Copy the circuit and apply it again to the target state. This will allow the phase amplifier to make another pass, and make the difference in the good answers' and bad answers' norms more pronounced
- Measure the first 4 qubits and isolate the eigenstates which turn up in the measurements most often. These eigenstates are the solutions to the Sudoku puzzle
Notice that we didn't give the circuit the answers to the Sudoku. We gave it the limiting conditions. These is a very fine distinction, but this is exactly what we would need to do for a really complex task where we don't know the answers beforehand.
Qiskit implementation
Here's how we do it in Qiskit. I took this circuit from the textbook, but expanded the oracle and the phase amplifier into the sequences of elementary gates:
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, assemble, Aer, execute
aer = Aer.get_backend("aer_simulator")
creg = ClassicalRegister(4, name="c")
qc = QuantumCircuit(QuantumRegister(9, name="q"), creg)
qc.h(8)
qc.z(8)
qc.h(0)
qc.h(1)
qc.h(2)
qc.h(3)
qc.cx(0, 4)
qc.cx(1, 4)
qc.cx(0, 5)
qc.cx(2, 5)
qc.cx(1, 6)
qc.cx(3, 6)
qc.cx(2, 7)
qc.cx(3, 7)
qc.mct([4, 5, 6, 7], 8)
qc.cx(0, 4)
qc.cx(1, 4)
qc.cx(0, 5)
qc.cx(2, 5)
qc.cx(1, 6)
qc.cx(3, 6)
qc.cx(2, 7)
qc.cx(3, 7)
qc.barrier()
qc.h(0)
qc.h(1)
qc.h(2)
qc.h(3)
qc.x(0)
qc.x(1)
qc.x(2)
qc.x(3)
qc.h(3)
qc.mct([0, 1, 2], 3)
qc.h(3)
qc.x(0)
qc.x(1)
qc.x(2)
qc.x(3)
qc.h(0)
qc.h(1)
qc.h(2)
qc.h(3)
qc.barrier()
qc.cx(0, 4)
qc.cx(1, 4)
qc.cx(0, 5)
qc.cx(2, 5)
qc.cx(1, 6)
qc.cx(3, 6)
qc.cx(2, 7)
qc.cx(3, 7)
qc.mct([4, 5, 6, 7], 8)
qc.cx(0, 4)
qc.cx(1, 4)
qc.cx(0, 5)
qc.cx(2, 5)
qc.cx(1, 6)
qc.cx(3, 6)
qc.cx(2, 7)
qc.cx(3, 7)
qc.barrier()
qc.h(0)
qc.h(1)
qc.h(2)
qc.h(3)
qc.x(0)
qc.x(1)
qc.x(2)
qc.x(3)
qc.h(3)
qc.mct([0, 1, 2], 3)
qc.h(3)
qc.x(0)
qc.x(1)
qc.x(2)
qc.x(3)
qc.h(0)
qc.h(1)
qc.h(2)
qc.h(3)
qc.measure([0, 1, 2, 3], creg)
qobj = assemble(qc)
aer_result = aer.run(qobj).result()
qc.draw()
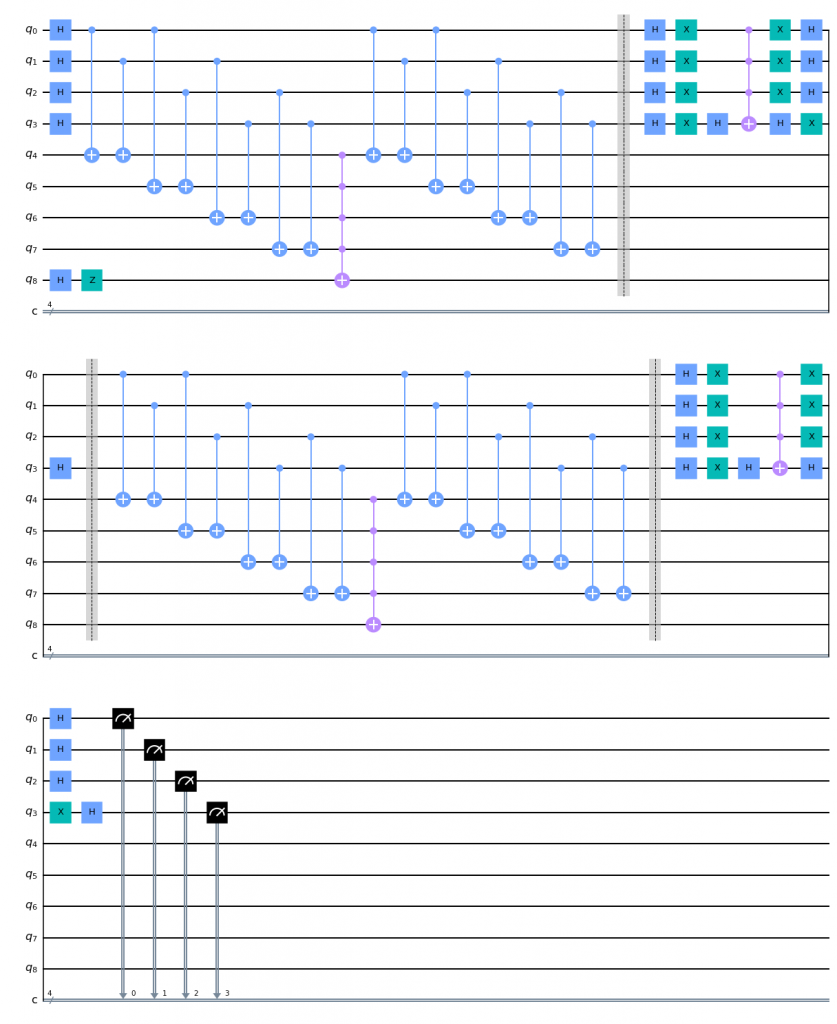
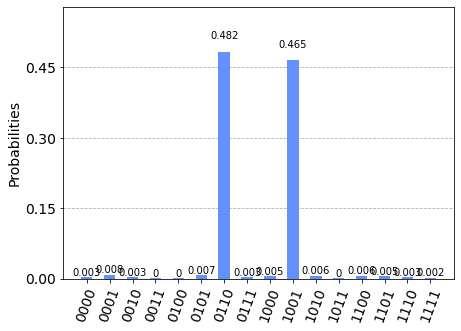
from qiskit.visualization import plot_histogram plot_histogram(aer_result.get_counts())
SQL implementation
And here's how we do it in SQL:
WITH RECURSIVE
settings AS
(
SELECT 9 AS qubits,
ARRAY[0, 1, 2, 3] AS measurements,
'
H: 8;
Z: 8;
H: 0;
H: 1;
H: 2;
H: 3;
CX: 0,4;
CX: 1,4;
CX: 0,5;
CX: 2,5;
CX: 1,6;
CX: 3,6;
CX: 2,7;
CX: 3,7;
CCCCX: 4,5,6,7,8;
CX: 0,4;
CX: 1,4;
CX: 0,5;
CX: 2,5;
CX: 1,6;
CX: 3,6;
CX: 2,7;
CX: 3,7;
H: 0;
H: 1;
H: 2;
H: 3;
X: 0;
X: 1;
X: 2;
X: 3;
H: 3;
CCCX: 0,1,2,3;
H: 3;
X: 0;
X: 1;
X: 2;
X: 3;
H: 0;
H: 1;
H: 2;
H: 3;
CX: 0,4;
CX: 1,4;
CX: 0,5;
CX: 2,5;
CX: 1,6;
CX: 3,6;
CX: 2,7;
CX: 3,7;
CCCCX: 4,5,6,7,8;
CX: 0,4;
CX: 1,4;
CX: 0,5;
CX: 2,5;
CX: 1,6;
CX: 3,6;
CX: 2,7;
CX: 3,7;
H: 0;
H: 1;
H: 2;
H: 3;
X: 0;
X: 1;
X: 2;
X: 3;
H: 3;
CCCX: 0,1,2,3;
H: 3;
X: 0;
X: 1;
X: 2;
X: 3;
H: 0;
H: 1;
H: 2;
H: 3;
' AS program
),
basis AS
(
SELECT eigenstate
FROM settings
CROSS JOIN
generate_series(0, (1 << qubits) - 1) AS eigenstate
),
gates (opcode, arity, matrix) AS MATERIALIZED
(
VALUES
('X', 1, ARRAY[
[0, 1],
[1, 0]
]::COMPLEX[][]),
('Y', 1, ARRAY[
[0, -(0, 1)],
[-(0, 1), 0]
]::COMPLEX[][]),
('Z', 1, ARRAY[
[1, 0],
[0, -1]
]::COMPLEX[][]),
('H', 1, ARRAY[
[1 / SQRT(2), 1 / SQRT(2)],
[1 / SQRT(2), -1 / SQRT(2)]
]::COMPLEX[][])
UNION ALL
SELECT REPEAT('C', arity - 1) || 'X', arity, matrix
FROM GENERATE_SERIES(2, 5) arity
CROSS JOIN LATERAL
(
WITH constants AS
(
SELECT (1 << (arity - 1)) - 1 AS mask,
(1 << arity) - 1 AS rank
)
SELECT ARRAY_AGG(cols ORDER BY row) AS matrix
FROM constants
CROSS JOIN LATERAL
(
SELECT row, ARRAY_AGG((CASE WHEN row & mask = mask AND col & mask = mask THEN row <> col ELSE row = col END)::INT::COMPLEX ORDER BY col) cols
FROM GENERATE_SERIES(0, rank) row
CROSS JOIN
GENERATE_SERIES(0, rank) col
GROUP BY
row
) gate
) toffoli
),
circuit AS MATERIALIZED
(
SELECT step, parts[1] AS opcode, inputs::INT[]
FROM settings
CROSS JOIN
REGEXP_SPLIT_TO_TABLE(program, E'\\s*;\\s*') WITH ORDINALITY instructions(instruction, step)
CROSS JOIN LATERAL
REGEXP_MATCHES(instruction, E'(\\w+)\\s*:\\s(.*)') parts
CROSS JOIN LATERAL
REGEXP_SPLIT_TO_ARRAY(parts[2], E'\\s*,\\s*') inputs
),
evolutions AS
(
SELECT 0 AS step, steps, state
FROM (
SELECT COUNT(*) AS steps
FROM circuit
) steps
CROSS JOIN
(
SELECT ARRAY_AGG((CASE eigenstate WHEN 0 THEN 1 ELSE 0 END)::COMPLEX ORDER BY eigenstate) AS state
FROM basis
) initial_state
UNION ALL
SELECT step + 1, steps, new_state.state
FROM evolutions
CROSS JOIN
settings
CROSS JOIN LATERAL
(
WITH circuit_gate AS MATERIALIZED
(
SELECT *
FROM circuit
WHERE circuit.step = evolutions.step + 1
),
gate AS MATERIALIZED
(
SELECT arity, matrix, inputs
FROM circuit_gate
JOIN gates
ON gates.opcode = circuit_gate.opcode
),
identity_qubits AS MATERIALIZED
(
SELECT ARRAY_AGG(input ORDER BY input) identity_qubits
FROM gate
CROSS JOIN LATERAL
(
SELECT input
FROM GENERATE_SERIES(0, qubits - 1) input
EXCEPT
SELECT input
FROM UNNEST(inputs) input
) q
),
unitary AS
(
SELECT circuit_identity_basis | circuit_gate_row_basis AS row,
circuit_identity_basis | circuit_gate_col_basis AS col,
coefficient
FROM gate
CROSS JOIN
identity_qubits
CROSS JOIN LATERAL
(
WITH circuit_gate_basis AS
(
SELECT gate_basis, circuit_gate_basis
FROM GENERATE_SERIES(0, (1 << arity) - 1) gate_basis
CROSS JOIN LATERAL
(
SELECT COALESCE(BIT_OR(1 << inputs[input + 1]), 0) AS circuit_gate_basis
FROM GENERATE_SERIES(0, arity - 1) input
WHERE gate_basis & (1 << input) > 0
) circuit_gate_basis
)
SELECT row.circuit_gate_basis AS circuit_gate_row_basis,
col.circuit_gate_basis AS circuit_gate_col_basis,
matrix[row.gate_basis + 1][col.gate_basis + 1]::COMPLEX AS coefficient
FROM circuit_gate_basis row
CROSS JOIN
circuit_gate_basis col
) circuit_gate_basis
CROSS JOIN LATERAL
(
SELECT circuit_identity_basis
FROM GENERATE_SERIES(0, (1 << (qubits - arity)) - 1) identity_basis
CROSS JOIN LATERAL
(
SELECT COALESCE(BIT_OR(1 << identity_qubit), 0) AS circuit_identity_basis
FROM UNNEST(identity_qubits) WITH ORDINALITY AS identity_qubits (identity_qubit, input)
WHERE identity_basis & (1 << (input - 1)::INT) > 0
) circuit_identity_basis
) circuit_identity_basis
WHERE coefficient <> 0::COMPLEX
),
state AS
(
WITH state AS
(
SELECT (r, i)::COMPLEX amplitude, ordinality - 1 AS eigenstate
FROM UNNEST(state) WITH ORDINALITY state (r, i, ordinality)
)
SELECT row, SUM(amplitude * coefficient) AS amplitude
FROM state
JOIN unitary
ON col = eigenstate
GROUP BY
row
)
SELECT ARRAY_AGG(amplitude ORDER BY row) state
FROM state
) new_state
WHERE step < steps
)
SELECT eigenstate_bits, probability
FROM (
SELECT state
FROM evolutions
WHERE step = steps
) state
CROSS JOIN
settings
CROSS JOIN LATERAL
(
WITH probabilities AS
(
SELECT norm((r, i)::COMPLEX) AS probability, ordinality - 1 AS eigenstate
FROM UNNEST(state) WITH ORDINALITY state(r, i, ordinality)
)
SELECT RIGHT(measurement_eigenstate::BIT(36)::TEXT, ARRAY_LENGTH(measurements, 1)) AS eigenstate_bits,
SUM(probability)::NUMERIC(4, 4) AS probability
FROM probabilities
CROSS JOIN LATERAL
(
SELECT BIT_OR(((eigenstate >> qubit) & 1) << position::INT - 1) AS measurement_eigenstate
FROM UNNEST(measurements) WITH ORDINALITY measurements (qubit, position)
) measurement
GROUP BY
measurement_eigenstate
) measurements
WHERE probability >= 0.0001
ORDER BY
probability DESC, eigenstate_bits
| eigenstate_bits | probability |
|---|---|
| 0110 | 0.4727 |
| 1001 | 0.4727 |
| 0000 | 0.0039 |
| 0001 | 0.0039 |
| 0010 | 0.0039 |
| 0011 | 0.0039 |
| 0100 | 0.0039 |
| 0101 | 0.0039 |
| 0111 | 0.0039 |
| 1000 | 0.0039 |
| 1010 | 0.0039 |
| 1011 | 0.0039 |
| 1100 | 0.0039 |
| 1101 | 0.0039 |
| 1110 | 0.0039 |
| 1111 | 0.0039 |
As we can see, our SQL quantum emulator runs in a fraction of a second and gives back the same answer that Qiskit's emulator does. The majority of experiments measure the first 4 qubits in the states |0110⟩ and |1001⟩, which correspond to the fields and
, which are indeed the answers to the binary Sudoku puzzle. It works!
You can view the queries here: https://github.com/quassnoi/explain-extended-2022
I wish you to be in perfect state in this New Year. May you only be entangled with people you love, may all probabilities be in your favor, and may all your measurements come out the way you expect.
Previous New Year posts:
 Subscribe in a reader
Subscribe in a reader
Every time I think we should shut the internet down, a post like this comes along and restores my faith in humanity. Cheers to you for even attempting something like this, let alone arriving at something that works.
Tony
1 Jan 22 at 10:29
Thank you!
Quassnoi
2 Jan 22 at 06:17
Wow
Witalij
11 Jan 22 at 14:33