EXPLAIN EXTENDED

Answering questions asked on the site.

Jason asks:

I have a co-worker who swears that Oracle IN queries are slow and refuses to use them. For example:

SELECT  foo
FROM    bar
WHERE   bar.stuff IN
(
SELECT  stuff
FROM    asdf
)

Typically, this kind of performance advice strikes me as overgeneralized and my instinct is to ignore it. But I figure I'll give him the benefit of the doubt and ask about it.

So, in general is an IN query very expensive? I'm having trouble putting together many non-trivial queries to run on EXPLAIN PLAN.

Does the IN predicate always have inferior efficiency compared to it's counterparts, EXISTS and JOIN?

Let's check.

First of all, there are at least three ways to check each row in a table against a list of (possible duplicate) values and return each row at most once:

• IN predicate:

  SELECT  foo
  FROM    bar
  WHERE   bar.stuff IN
  (
  SELECT  stuff
  FROM    asdf
  )
  

• EXISTS predicate:

  SELECT  foo
  FROM    bar
  WHERE   EXISTS
  (
  SELECT  NULL
  FROM    asdf
  WHERE   asdf.stuff = bar.stuff
  )
  

• JOIN / DISTINCT:

  SELECT  b.foo
  FROM    (
  SELECT  DISTINCT stuff
  FROM    asdf
  ) a
  JOIN    bar b
  ON      b.stuff = a.stuff
  

All these queries are semantically the same.

Common wisdom advices against using IN predicates because it just doesn't look a right thing to do.

This is because less experienced SQL developers tend to translate the SQL statements into pseudocode just like they see it, which in this case looks something like this:

foreach ($bar as $bar_record) {
foreach ($asdf as $asdf_record) {
if ($bar_record->stuff == $asdf_record->stuff)
output ($bar_record);
break;
}
}

This just radiates inefficiency, since the inner rowset should be iterated for each row returned.

EXISTS looks more nice since it at least gives a hint of possibility to use an index. However, it still looks like the same nested loops.

Finally, the JOIN looks the most promising here since everybody knows joins are optimized (though few know how exactly). But an IN? No thanks, they say, it will execute once for every row, it's slow, it's bad, it's inefficient!

People, come on. Oracle developers have thought it over ages ago and guess what: they turned out to be smart enough to implement an efficient algorithm for an IN construct.

Now, let's make two sample tables and see how it's done:
Read the rest of this entry »

Continuing the series:

What is better to store hierarchical data: nested sets model or adjacency list (parent-child) model?

For detailed explanations of the terms, see the first article in the series:

• Adjacency list vs. nested sets: PostgreSQL

This is the last article of the series which covers MySQL.

MySQL differs from the other systems, since it is the only system of the big four that does not support recursion natively. It has neither recursive CTE's nor CONNECT BY clause, not even rowset returning functions that help to emulate recursion in PostgreSQL 8.3.

MySQL supports a thing that all other systems either lack or implement inefficiently: session variables. They can be set in a SELECT clause and can be used to keep some kind of a state between the rows as they are processed and returned in a rowset.

This of course is against the whole spirit of SQL, since SQL implies operations on whole sets and session variables operate on rows and are totally dependent on the order they are returned or processed. But if used properly, this behavior can be exploited to emulate some things that MySQL lacks: analytic functions, efficient random row sampling etc.

Hierarchical functions are among the things that need to be emulated in MySQL using session variables to keep the function state.

Here's the old article in my blog that shows how to do this:

• Hierarchical queries in MySQL

On the other hand, MySQL implements one more thing that is useful for nested sets model: SPATIAL indexes.
Read the rest of this entry »

Continuing the series:

What is better to store hierarchical data: nested sets model or adjacency list (parent-child) model?

For detailed explanations of the terms, see the first article in the series:

• Adjacency list vs. nested sets: PostgreSQL

Today is Oracle time.

Adjacent sets require recursion, and Oracle has a native way to implement recursion in SQL statements. To do this it uses a special clause, CONNECT BY.

Unlike other systems, Oracle always supported recursion in SQL statements since version 2 (this is the name the first version of Oracle was released under).

This was done because by that time there already were several hierarchical databases on the market which are quite good for storing hierarchical data. If not for this clause, transition from a hierarchical DBMS to the relational DBMS would be too hard.

Oracle's way to query self-relations is somewhat different from recursive CTE's that other systems use:

• Recursive CTEs can use an arbitrary set in recursive steps. The recursion base and recursion stack are not visible in further steps. The recursive operation is a set operation (usually a JOIN) on the recursion parameter (a set) and the result of the previous operation:

  

• CONNECT BY queries can only use the value of a single row in recursive steps.

  The recursion base and recursion stack are visible, the values outside the recursion stack are not.

  The recursive operation is a set operation on each row of the current row and the base rowset.

  Unlike recursive CTE, CONNECT BY operates row-wise, that is each row of the result spans its own recursion branch with its own stack: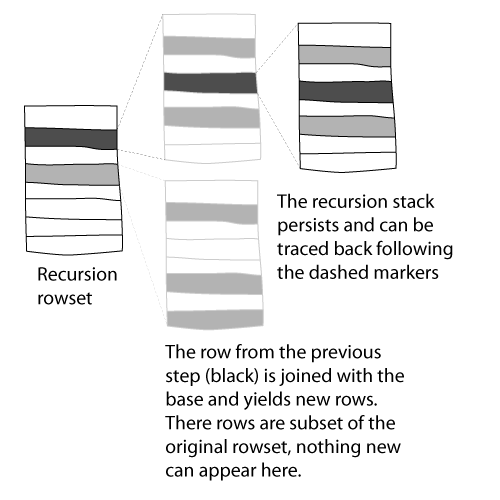

  

The main difference it that the CONNECT BY operation cannot produce anything that was not in the original rowset, while a recursive CTE can.

However, CONNECT BY has numerous benefits too: it's very fast, allows to track the hierarchy path easily (using a built-in funtion named SYS_CONNECT_BY_PATH) and implicitly sorts the recordset in tree order (with additional clause ORDER SIBLINGS BY to sort the siblings).

This method, of course, allows traversing adjacency lists easily.

To compare efficiency of adjacency lists and that of nested sets, let's create a sample table:
Read the rest of this entry »

Continuing the series:

What is better to store hierarchical data: nested sets model or adjacency list (parent-child) model?

For detailed explanations of the terms, see the first article in the series:

• Adjacency list vs. nested sets: PostgreSQL

Now, let's see what's better for SQL Server.

We will create a single table that holds both adjacency list data and nested sets data, with 8 levels of nesting, 5 children of each parent node and 2,441,405 records:
Read the rest of this entry »

This series of articles is inspired by numerous questions asked on the site and on Stack Overflow.

What is better to store hierarchical data: nested sets model or adjacency list (parent-child) model?

First, let's explain what all this means.

Adjacency list

Hierarchical relations (not to be confused with hierarchical data model) are 0-1:0-N transitive relations between entities of same domain.

For instance, ancestor-descendant relation is:

• Transitive:
  • If A is an ancestor of B and B is an ancestor of C, then A is an ancestor of C
• Antisymmetric:
  • If A is an ancestor of B, then B is never an ancestor of A
• Irreflexive:
  • A is never an ancestor to itself
• 0-1:0-N
  • A can have zero, one or many children. A can have zero or one parents.

These relations can be represented by an ordered directed tree.

Tree is a simple directed graph (that with at most one directed edge between two different vertices) and relational model has means to represent simple graphs.

Two vertices are considered related (and therefore their primary keys forming a row in the table) if and only if they are connected with an edge.

This table along with the table defining the vertices identifies a graph completely by defining pairs of vertices connected by the edges. Each record in the table defines a pair of adjacent vertices, that's why this representation is called adjacency list.

Adjacency lists can represent any simple directed graphs, not ony hierarchy trees. But due to the fact that this structure is most commonly used to define the parent-child relationships, the terms parent-child model and adjacency list model have almost become synonymous. However, they are not: adjacency list model is much wider and parent-child model is one of its implementations.

Now, since we have a tree here which implies 0-1:0-N relationship between the vertices, we can define the relation as a self-relation: the table defines both the entity and the relationship. Parent is just a one attribute among other attributes with a FOREIGN KEY reference to the table itself.

Since multple items can have no parents (and therefore be the roots of their trees), it's sometimes useful to convert this tree into an arborescence: make a single fake root that considered a parent of all entries that have no actual parent.

This is a nice and elegant model, but until recently it had one drawback: it could not be used with SQL.
Read the rest of this entry »

Answering questions asked on the site.

Cora asks:

I want to build an alphabetical index over the articles in my database.

I need to show 5 entries in the index, like this: A-D, E-F etc., so that each entry contains roughly equal number of articles.

How do I do it in a single query?

This is in Oracle

This is a good task to demonstrate Oracle's analytic abilities.

To do this, we will create a sample table:
Read the rest of this entry »

From Stack Overflow:

I've got a set of data that contains users, their awards and the time they are granted.

When a user earns an award, the award and user is logged along with a date.

What I'd like is a query that finds a set of 3 achievements that were earned within 5 minutes of each other by the same user.

Any thoughts on how to accomplish this?

I'll go a step further and try to build a general solution to find sets of N values within a given time frame.

We should return all rows that are parts of all 5-minute time frames containing at least N values. These timeframes can overlap.

We should build such a timeframe for each record, make sure that there are at least N values in this timeframe, and if yes, return these values (applying DISTINCT to get rid of the duplicates).

Let's create a sample table and build a query to do this:

Read the rest of this entry »

From Stack Overflow:

I'm looking for a way to round every value contained in a column without changing the total sum (which is known to be an integer, or very close to an integer because of float number precision).

Rounding every value to the nearest integer won't work (ex : (1.5, 1.5) will be rounded to either (1, 1) or (2, 2))

It's quite easy to do this using several requests (e. g. storing the original sum, rounding, computing the new sum, and updating as many rows as needed to go back to the original sum), but this is not a very elegant solution.

Is there a way to do this using a single SQL request?

I'm using SQL Server 2008, so solutions taking advantage of this specific vendor are welcome.

I'm looking for a request minimizing the differences between the old values and the new ones. In other words, a value should never be rounded up if a greater value has been rounded down, and vice-versa

We have two restrictions here:

1. The sum of the rounded numbers should be equal to that of the unrounded ones.
2. When rounding, no number with a greater fractional part can be rounded down if there is a number with a smaller fractional part that had been rounded up.

We cannot round (1.4, 1.4, 1.2) to (1, 1, 2), since 1.4 would be rounded down while 1.2 (with smaller fractional part) is rounded up. However, we can round them to (1, 2, 1) or (1, 2, 1), since nothing prevents us from rounding numbers with equal fractional part differently.

Given this, we should build a query that would take a set of numbers and round them taking these two restrictions into account.

It is easily seen than to satisfy the second restriction a certain rounding threshold should exist: all numbers with the fractional part greater than this threshold are rounded up, those with the fractional part smaller than then threshold are rounded down, those with the fractional part equal to the threshold can be rounded both ways.

However, calculating this threshold is, first, quite a difficult task and, second, we still don't know what to do with the numbers having the fractional part equal to the threshold.

Instead, we use another approach.

Let's create a sample tables and show this approach:

Read the rest of this entry »

Which method is best to select values present in one table but missing in another one?

This:

SELECT  l.*
FROM    t_left l
LEFT JOIN
        t_right r
ON      r.value = l.value
WHERE   r.value IS NULL

, this:

SELECT  l.*
FROM    t_left l
WHERE   l.value NOT IN
        (
        SELECT  value
        FROM    t_right r
        )

or this:

SELECT  l.*
FROM    t_left l
WHERE   NOT EXISTS
        (
        SELECT  NULL
        FROM    t_right r
        WHERE   r.value = l.value
        )

Finally, it's MySQL time.

As always, we will create the sample tables:

Read the rest of this entry »

Which method is best to select values present in one table but missing in another one?

This:

SELECT  l.*
FROM    t_left l
LEFT JOIN
t_right r
ON      r.value = l.value
WHERE   r.value IS NULL

, this:

SELECT  l.*
FROM    t_left l
WHERE   l.value NOT IN
(
SELECT  value
FROM    t_right r
)

or this:

SELECT  l.*
FROM    t_left l
WHERE   NOT EXISTS
(
SELECT  NULL
FROM    t_right r
WHERE   r.value = l.value
)

Today, we will see how Oracle copes with these queries.

And to do this, we, of course, should create sample tables:

Read the rest of this entry »