EXPLAIN EXTENDED

How to create fast database queries

Efficient circle distance testing

Comments enabled. I *really* need your comment

Answering questions asked on the site.

eptil asks:

I am using SQL Server 2008, but not the spatial features.

I have a table with few entries, only 40,000. There is an id INT PRIMARY KEY column and two columns storing a 2d coordinate, both decimals.

I would like to find all the records that do not have other records within a given radius. The query I am using at the moment is:

SELECT  id, x, y
FROM    mytable t1
WHERE   (
        SELECT  COUNT(*)
        FROM    mytable t2
        WHERE   ABS(t1.x - t2.x) < 25
                AND ABS(t1.y - t2.y) < 25
        ) = 1
&#91;/sourcecode&#93;
<!-- -->
This is taking <strong>15</strong> minutes to run at times.

Is there a better way?
</blockquote>

Of course using spatial abilities would be a better way, but it is possible to make do with plain <strong>SQL</strong>. This will also work in <strong>SQL Server 2005</strong>.

In most database engines, the spatial indexes are implemented as the <strong>R-Tree</strong> structures. <strong>SQL Server</strong>, however, uses another approach: surface tesselation.

Basically, it divides the surface into a finite number of tiles, each assigned with a unique number. The identifiers of tiles covered by the object are stored as keys of a plain <strong>B-Tree</strong> index.

When <strong>SQL Server</strong>'s optimizer sees a geometrical predicate against an indexed column, it calculates the numbers of tiles that <em>possibly</em> can satisfy this predicate. Say, if the tiles are defined as squares with side <strong>1</strong>, the predicate <code>column.STDistance(@mypoint) &lt; 2</code> can only be satisfied by the objects within <strong>2</strong> tiles away from <code>@mypoint</code>'s tile. This gives a square of <strong>25</strong> tiles with <code>@mypoint</code>'s tile in the center. The tile numbers can be found and searched for using the index. Exact filtering condition is then applied to each candidate value returned by the index.

Same solution can be used in our case even without the spatial functions. Comparing tile numbers is an equijoin and hash join method is eligible for this operation. We can even choose the tiling algorithm individually for each query, since we don't have to store the tile identifiers in the table, and the hash table will be built dynamically anyway.

Let's create a sample table and see how it works:
<span id="more-4449"></span>

CREATE SCHEMA [20100226_circle]
CREATE TABLE t_circle (
        id INT NOT NULL PRIMARY KEY,
        x DECIMAL (15, 3) NOT NULL, 
        y DECIMAL (15, 3) NOT NULL,
        )
GO
BEGIN TRANSACTION
SELECT  RAND(20100226)
DECLARE @cnt INT
SET @cnt = 1
WHILE @cnt <= 50000
BEGIN
        INSERT
        INTO    &#91;20100226_circle&#93;.t_circle (id, x, y)
        VALUES  (
                @cnt,
                RAND() * 3200,
                RAND() * 3200
                )
        SET @cnt = @cnt + 1
END
COMMIT
GO
&#91;/sourcecode&#93;

The table contains <strong>50,000</strong> points on random places within a square of <strong>3,200 &times; 3,200</strong> units.

We can optimize the original query a little by using <code>NOT EXISTS</code> instead of <code>COUNT(*)</code>:


SELECT  *
FROM    [20100226_circle].t_circle co
WHERE   NOT EXISTS
        (
        SELECT  NULL
        FROM    [20100226_circle].t_circle ci
        WHERE   SQRT(POWER(co.x - ci.x, 2) + POWER(co.y - ci.y, 2)) < 25
                AND co.id <> ci.id
        )
ORDER BY
        id

View query results

, but this would still be quite slow.

The problem is that the nested loops go nowhere: they are still inside the plan, but return earlier. As a result, the query takes 5 minutes instead of 15, which is still too much.

To improve the query we need to make an efficient anti-join method to work, and the tesselation strategy is a way to go. Here's what we need to do to implement this strategy:

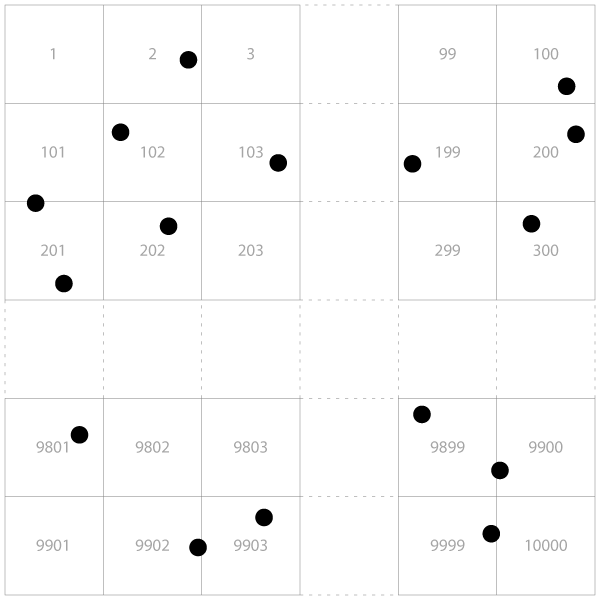
  • Tesselate the surface and assign a unique number to each tile. Since we need to search for the records within 25 units, it will be a reasonable idea to divide the surface into a number of squares 25 × 25 units in size, numbered column-wise. To find out the number of rows and columns, we should just find the MIN and MAX x and y.

    This is the sample tesselation, assuming that MIN(x) and MIN(y) are 25 × 100 = 2500 units apart (and same with y).

  • Find the tile each point belongs to.

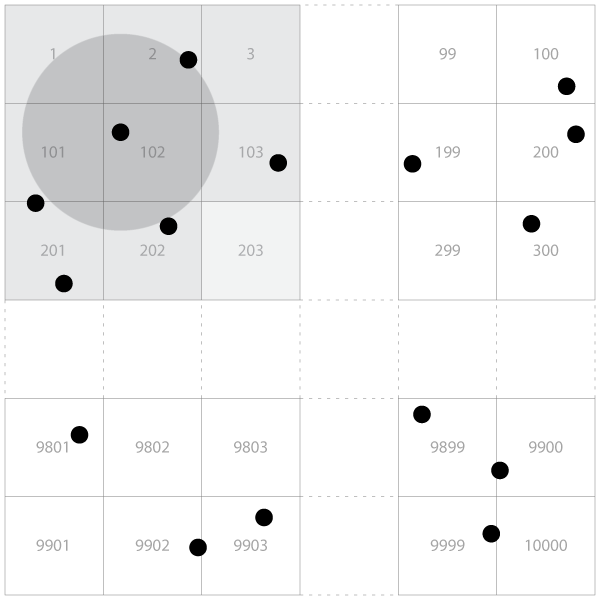
  • Build a recordset that would correspond each point to each of the tiles the neighbors can theoretically reside in. Since a circle with radius of 25 units theoretically may cover up to 9 adjacent tiles, each tile should be corresponded to each of the 9 tiles forming a 3 × 3 square with a unit's tile in the center.

  • For each point, make sure that no other points exists within the neighboring tiles, additionally applying a fine-filtering condition.

    This may sound redundant, since the point-neighbor combination is unique, as well as point-tile, so only one of the 9 candidates will satisfy the join, even if the points reside in the adjacent tiles. But finding the exact distance requires a complex expression while comparing the tile numbers is an equality correlation and as such is eligible by an efficient anti-join method like HASH ANTI JOIN. The coarse filtering on tiles will sieve out most of the far neighbors so that the only adjacent neighbors will require special attention.

And here's the query:

WITH extremes AS
(
SELECT *,
maxx - minx AS width,
maxy - miny AS height
FROM (
SELECT FLOOR(MIN(x) / 25) AS minx,
CEILING(MAX(x) / 25) AS maxx,
FLOOR(MIN(y) / 25) AS miny,
CEILING(MAX(y) / 25) AS maxy
FROM [20100226_circle].t_circle
) q
),
tileset (dim) AS
(
SELECT -1
UNION ALL
SELECT 0
UNION ALL
SELECT 1
),
tiles AS
(
SELECT id, x, y, minx, miny, width,
(FLOOR(x / 25) - minx) * width + FLOOR(y / 25) - miny AS tile
FROM extremes
CROSS JOIN
[20100226_circle].t_circle
),
neighbors AS
(
SELECT ti.*,
(FLOOR(ti.x / 25) - ti.minx + nx.dim) * ti.width +
FLOOR(ti.y / 25) - ti.miny + ny.dim AS mtile
FROM tiles ti
CROSS JOIN
tileset nx
CROSS JOIN
tileset ny
)
SELECT *
FROM tiles tn
WHERE NOT EXISTS
(
SELECT NULL
FROM neighbors n
WHERE n.mtile = tn.tile
AND n.id <> tn.id
AND SQRT(SQUARE(n.x - tn.x) + SQUARE(n.y - tn.y)) < 25 ) ORDER BY id [/sourcecode]

id x y minx miny width tile
205 2247.896 3198.399 0 0 128 11519
2867 2159.626 1120.590 0 0 128 11052
13644 4.951 3165.734 0 0 128 126
15917 2747.826 3041.280 0 0 128 14073
25183 1858.866 326.416 0 0 128 9485
43211 1176.369 98.079 0 0 128 6019
6 rows fetched in 0.0017s (3.0781s) 
Table 't_circle'. Scan count 11, logical reads 3087, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0. 
Table 'Worktable'. Scan count 2, logical reads 207406, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0. 
Table 'Worktable'. Scan count 0, logical reads 0, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0. 

SQL Server Execution Times:
   CPU time = 4235 ms,  elapsed time = 3068 ms. 

  |--Parallelism(Gather Streams, ORDER BY:([test].[20100226_circle].[t_circle].[id] ASC))
       |--Sort(ORDER BY:([test].[20100226_circle].[t_circle].[id] ASC))
            |--Compute Scalar(DEFINE:([Expr1007]=floor([Expr1003]/(25.)), [Expr1009]=floor([Expr1005]/(25.)), [Expr1011]=ceiling([Expr1004]/(25.))-floor([Expr1003]/(25.)), [Expr1016]=(([Expr1044]-floor([Expr1003]/(25.)))*(ceiling([Expr1004]/(25.))-floor([Expr1003]/(25.)))+[Expr1045])-floor([Expr1005]/(25.))))
                 |--Hash Match(Left Anti Semi Join, HASH:([Expr1055])=([Expr1054]), RESIDUAL:([Expr1054]=[Expr1055] AND [test].[20100226_circle].[t_circle].[id]<>[test].[20100226_circle].[t_circle].[id] AND sqrt(square(CONVERT_IMPLICIT(float(53),[test].[20100226_circle].[t_circle].[x]-[test].[20100226_circle].[t_circle].[x],0))+square(CONVERT_IMPLICIT(float(53),[test].[20100226_circle].[t_circle].[y]-[test].[20100226_circle].[t_circle].[y],0)))<(2.500000000000000e+001)))
                      |--Bitmap(HASH:([Expr1055]), DEFINE:([Bitmap1056]))
                      |    |--Parallelism(Repartition Streams, Hash Partitioning, PARTITION COLUMNS:([Expr1055]))
                      |         |--Compute Scalar(DEFINE:([Expr1055]=(([Expr1044]-floor([Expr1003]/(25.)))*(ceiling([Expr1004]/(25.))-floor([Expr1003]/(25.)))+[Expr1045])-floor([Expr1005]/(25.))))
                      |              |--Nested Loops(Inner Join)
                      |                   |--Parallelism(Distribute Streams, Broadcast Partitioning)
                      |                   |    |--Stream Aggregate(DEFINE:([Expr1003]=MIN([partialagg1048]), [Expr1004]=MAX([partialagg1049]), [Expr1005]=MIN([partialagg1050])))
                      |                   |         |--Parallelism(Gather Streams)
                      |                   |              |--Stream Aggregate(DEFINE:([partialagg1048]=MIN([test].[20100226_circle].[t_circle].[x]), [partialagg1049]=MAX([test].[20100226_circle].[t_circle].[x]), [partialagg1050]=MIN([test].[20100226_circle].[t_circle].[y])))
                      |                   |                   |--Clustered Index Scan(OBJECT:([test].[20100226_circle].[t_circle].[PK__t_circle__62065FF3]))
                      |                   |--Compute Scalar(DEFINE:([Expr1044]=floor([test].[20100226_circle].[t_circle].[x]/(25.)), [Expr1045]=floor([test].[20100226_circle].[t_circle].[y]/(25.))))
                      |                        |--Clustered Index Scan(OBJECT:([test].[20100226_circle].[t_circle].[PK__t_circle__62065FF3]))
                      |--Parallelism(Repartition Streams, Hash Partitioning, PARTITION COLUMNS:([Expr1054]), WHERE:(PROBE([Bitmap1056])=TRUE))
                           |--Compute Scalar(DEFINE:([Expr1054]=(((([Expr1046]-floor([Expr1020]/(25.)))+CONVERT_IMPLICIT(decimal(10,0),[Union1037],0))*(ceiling([Expr1021]/(25.))-floor([Expr1020]/(25.)))+[Expr1047])-floor([Expr1022]/(25.)))+CONVERT_IMPLICIT(decimal(10,0),[Union1041],0)))
                                |--Nested Loops(Inner Join)
                                     |--Nested Loops(Inner Join)
                                     |    |--Parallelism(Distribute Streams, RoundRobin Partitioning)
                                     |    |    |--Nested Loops(Inner Join)
                                     |    |         |--Stream Aggregate(DEFINE:([Expr1020]=MIN([partialagg1051]), [Expr1021]=MAX([partialagg1052]), [Expr1022]=MIN([partialagg1053])))
                                     |    |         |    |--Parallelism(Gather Streams)
                                     |    |         |         |--Stream Aggregate(DEFINE:([partialagg1051]=MIN([test].[20100226_circle].[t_circle].[x]), [partialagg1052]=MAX([test].[20100226_circle].[t_circle].[x]), [partialagg1053]=MIN([test].[20100226_circle].[t_circle].[y])))
                                     |    |         |              |--Clustered Index Scan(OBJECT:([test].[20100226_circle].[t_circle].[PK__t_circle__62065FF3]))
                                     |    |         |--Constant Scan(VALUES:(((-1)),((0)),((1))))
                                     |    |--Constant Scan(VALUES:(((-1)),((0)),((1))))
                                     |--Table Spool
                                          |--Compute Scalar(DEFINE:([Expr1046]=floor([test].[20100226_circle].[t_circle].[x]/(25.)), [Expr1047]=floor([test].[20100226_circle].[t_circle].[y]/(25.))))
                                               |--Clustered Index Scan(OBJECT:([test].[20100226_circle].[t_circle].[PK__t_circle__62065FF3]))

This query only takes 3 seconds.

Hope that helps.

I'm always glad to answer the questions regarding database queries.

Ask me a question

Written by Quassnoi

February 26th, 2010 at 11:00 pm

Posted in SQL Server

«
»

Leave a Reply