Sargability of monotonic functions: example
In my previous article I presented a proposal to add sargability of monotonic functions into the SQL engines.
In a nutshell: a monotonic function is a function that preserves the order of the argument so that it gives the larger results for the larger values of the argument. It is easy to prove that a B-tree with each key replaced by the result of the function will remain the valid B-Tree and hence can be used to search for ranges of function results just like it is used to search for ranges of values.
With a little effort, a B-Tree can also be used to search for the ranges of piecewise monotonic functions: those whose domain can be split into a number of continuous pieces with the function being monotonic within each piece (but it may be not monotonic and even not continuous across the pieces).
In this article, I'll demonstrate the algorithm to do that (implemented in pure SQL on PostgreSQL).
I will show how the performance of simple query
SELECT * FROM t_sine WHERE SIN(value) BETWEEN 0.1234 AND 0.1235
could be improved if the sargability of monotonic functions had been implemented in the optimizer.
To do this, I will create a sample table:
CREATE TABLE t_sine (
id INT NOT NULL PRIMARY KEY,
value DOUBLE PRECISION NOT NULL
);
CREATE INDEX ix_sine_value ON t_sine (value);
SELECT SETSEED(0.20100223);
INSERT
INTO t_sine
SELECT num, num / 10000.00 + RANDOM()
FROM generate_series(1, 1000000) num;
ANALYZE t_sine;
This table contains 1,000,000 records with value randomly distributed from 0 to 101.
To select the records we need, we can use a very simple and straightforward query:
SELECT * FROM t_sine WHERE SIN(value) BETWEEN 0.4452 AND 0.4453
| id | value | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3663 | 0.46150185738802 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19263 | 2.68015610060766 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23783 | 2.68013202354237 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86110 | 8.963312032599 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 128053 | 13.0278523004308 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 150339 | 15.2465362691633 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 185849 | 19.310986539682 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 186788 | 19.3110526885197 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 191391 | 19.3110088731334 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 210841 | 21.5297331408583 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 212511 | 21.529697893659 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 247639 | 25.5941842560224 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 373019 | 38.1605504324339 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 373416 | 38.1606072025172 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 458141 | 46.6624391236514 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 462683 | 46.6623900452435 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 462704 | 46.662440645238 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 463233 | 46.6624209528782 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 520118 | 52.945639446865 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 522686 | 52.9456708737895 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 561721 | 57.0100855686799 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 686886 | 69.5764806582652 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 711952 | 71.7951245983548 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 716508 | 71.7952263388403 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 778116 | 78.0783171531357 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 877138 | 88.4260205388732 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 903050 | 90.6446926224232 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 942345 | 94.7092782433405 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 946181 | 94.7092303088069 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 966815 | 96.9279387165383 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 999931 | 100.992433886895 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 rows fetched in 0.0022s (3.2500s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Seq Scan on t_sine (cost=0.00..25406.00 rows=5000 width=12) Filter: ((sin(value) >= 0.4452::double precision) AND (sin(value) <= 0.4453::double precision))
which returns 31 records in 3.25 seconds.
The query uses a full table scan with the filter applied to each record.
Let's try to improve it.
Function description
According to the notation I proposed in the previous article, the monotony of the function SIN() should be described as this:
SIN(arg FLOAT) MONOTONIC PIECEWISE
DEFINED BY FLOOR(arg / PI() + 0.5)
CASE PIECE % 2
WHEN 0 THEN DECREASING INVERSE PIECE * PI() + ASIN(RESULT)
ELSE INCREASING INVERSE PIECE * PI() - ASIN(RESULT)
END
This means that:
-
The function is piecewise monotonic,
-
The pieces are defined by the function
FLOOR(arg / PI() + 0.5)(which essentially returns the number of the half-wave the argument belongs too), -
The function monotony varies depending on the piece,
-
On odd pieces, the function increases,
-
On even pieces, the function decreases.
-
A single inverse expression is provided for each monotony
Note that mathematically the function is strictly monotonic on each of its pieces. However, due to the rounding errors, different arguments can yield same function results, so the function value may map back to a range of the arguments rather than a single value.
In theory, it is possible to write a single expression which would map the function's result to the pair of values defining the beginning and the end of such a range. However, the expression would be quite complex. So for illustration purposes I'll make do with a single inverse function that yields an approximation of the back mapping. To find the exact range, some extra effort will be required.
Building the pieces
The function is piecewise monotonic and the pieces are defined by a function. For the pieces to be continuous, the function that defines them should be itself monotonic over all its domain.
The function that defines the pieces is FLOOR(arg / PI() + 0.5).
It is a superposition of the three functions:
-
OPERATOR_DIVISION(arg1 FLOAT, arg2 FLOAT)
MONOTONIC OVER (arg1)
CASE WHEN arg2 > 0 THEN INCREASING INVERSE RESULT * arg2
WHEN arg2 = 0 THEN UNDEFINED
WHEN arg2 < 0 THEN DECREASING INVERSE RESULT * arg2 END -
OPERATOR_PLUS(arg1 FLOAT, arg2 FLOAT) MONOTONIC
OVER (arg1) STRICTLY INCREASING INVERSE RESULT - arg2,
OVER (arg2) STRICTLY INCREASING INVERSE RESULT - arg1 -
FLOOR(arg FLOAT) MONOTONIC INCREASING
INVERSE
FROM RESULT EXACT
TO RESULT + 1 EXACT EXCLUDE
which are, given the values of the constants provided in the secondary arguments, are increasing over the argument. As we know from math, a superposition of monotonic functions is also monotonic.
Each function is defined with a single inverse condition which maps the result of the function back to a value near the range of the arguments yielding the result. The exact range has to be sought for using index seek over (hopefully) not too many records.
Sequentially applying the inverse expressions of each of the constituent functions to the result of the piece defining function, we get the following inverse expression for the latter:
FLOOR(OPERATOR_PLUS(OPERATOR_DIVISION(arg, PI()), 0.5)) = PIECEOPERATOR_PLUS(OPERATOR_DIVISION(arg, PI()), 0.5) ∈ [ PIECE, PIECE + 1 )OPERATOR_DIVISION(arg, PI()) ∈ [ ≈(PIECE - 0.5), ≈((PIECE + 1) - 0.5) ]arg ∈ [ ≈((PIECE - 0.5) * PI()), ≈(((PIECE + 1) - 0.5) * PI()) ]
For each piece, we how have a pair of values approximately defining the range of values belonging to the piece.
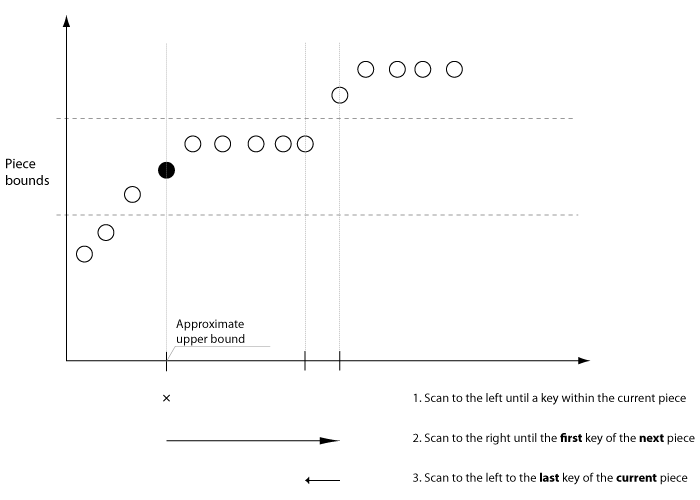
To find out the exact bounds, we need to do the following:
-
Calculate the piece for the minimal
value -
Find the approximate upper bound for the piece.
-
Scanning the keys to the left, find the rightmost key to the left of the upper bound that belongs to the current (or previous) piece.
-
Scanning the keys to the right, find the first key of the next piece.
-
Scanning a single key to the left, find the last key of the current piece.
-
Recursively repeat steps 1 to 5, taking the first value the next piece calculated on step 4 as a seed for the step 1, until step 4 fails (which means that the pieces are over).
This procedure guarantees that we always get the correct bounds even with the inexact inverse value, since it correctly handles both overflow and underflow of the inverse value, as show on the pictures below:
Overflow

Underflow
Here's a query that selects the first and the last key of each piece:
WITH RECURSIVE
d AS (
SELECT piece,
minv,
COALESCE(
(
SELECT value
FROM t_sine
WHERE value < nv[1]
ORDER BY
value DESC
LIMIT 1
),
(
SELECT MAX(value)
FROM t_sine
)
) AS maxv,
nv[1] AS nextv,
nv[2] AS nextpiece
FROM (
SELECT minv, piece,
(
SELECT ARRAY[value, FLOOR(value / PI() + 0.5)]
FROM t_sine
WHERE value >
(
SELECT value
FROM t_sine
WHERE value <= ((piece + 1) - 0.5) * PI()
AND FLOOR(value / PI() + 0.5) <= piece
ORDER BY
value DESC
LIMIT 1
)
ORDER BY
value
LIMIT 1
) nv
FROM (
SELECT minv, FLOOR(minv / PI() + 0.5) AS piece
FROM (
SELECT MIN(value) AS minv
FROM t_sine
) q
) q2
) q3
UNION ALL
SELECT piece,
minv,
COALESCE(
(
SELECT value
FROM t_sine
WHERE value < nv[1]
ORDER BY
value DESC
LIMIT 1
),
(
SELECT MAX(value)
FROM t_sine
)
) AS maxv,
nv[1] AS nextv,
nv[2] AS nextpiece
FROM (
SELECT minv, piece,
(
SELECT ARRAY[value, FLOOR(value / PI() + 0.5)]
FROM t_sine
WHERE value >
(
SELECT value
FROM t_sine
WHERE value <= ((piece + 1) - 0.5) * PI()
AND FLOOR(value / PI() + 0.5) <= piece
ORDER BY
value DESC
LIMIT 1
)
ORDER BY
value
LIMIT 1
) nv
FROM (
SELECT nextv AS minv, nextpiece AS piece
FROM d
WHERE nextpiece IS NOT NULL
) q2
) q3
)
SELECT *
FROM d
[/sourcecode]
<div class="terminal">
<table class="terminal">
<tr>
<th>piece</th><th>minv</th><th>maxv</th><th>nextv</th><th>nextpiece</th></tr>
<tr><td class="float8">0</td><td class="float8">0.0172837972298265</td><td class="float8">1.57060804706216</td><td class="float8">1.57081433883309</td><td class="float8">1</td></tr>
<tr><td class="float8">1</td><td class="float8">1.57081433883309</td><td class="float8">4.7123523916252</td><td class="float8">4.71268981658742</td><td class="float8">2</td></tr>
<tr><td class="float8">2</td><td class="float8">4.71268981658742</td><td class="float8">7.85390641669333</td><td class="float8">7.85409013534784</td><td class="float8">3</td></tr>
<tr><td class="float8">3</td><td class="float8">7.85409013534784</td><td class="float8">10.9955484666698</td><td class="float8">10.9956333589859</td><td class="float8">4</td></tr>
<tr><td class="float8">4</td><td class="float8">10.9956333589859</td><td class="float8">14.1371444690436</td><td class="float8">14.1372372000463</td><td class="float8">5</td></tr>
<tr class="break"><td colspan="100"/></tr>
<tr><td class="float8">31</td><td class="float8">95.8185816861346</td><td class="float8">98.9601405610755</td><td class="float8">98.9601765494391</td><td class="float8">32</td></tr>
<tr><td class="float8">32</td><td class="float8">98.9601765494391</td><td class="float8">100.992433886895</td><td class="float8"></td><td class="float8"></td></tr>
<tr class="statusbar"><td colspan="100">33 rows fetched in 0.0057s (0.0484s)</td></tr>
</table>
</div>
<pre>
CTE Scan on d (cost=65.97..67.99 rows=101 width=40)
CTE d
-> Recursive Union (cost=0.08..65.97 rows=101 width=16)
-> Subquery Scan q (cost=0.08..0.80 rows=1 width=8)
InitPlan 5 (returns $5)
-> Result (cost=0.03..0.04 rows=1 width=0)
InitPlan 4 (returns $4)
-> Limit (cost=0.00..0.03 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..33799.01 rows=1000000 width=8)
Filter: (value IS NOT NULL)
-> Result (cost=0.03..0.04 rows=1 width=0)
InitPlan 10 (returns $8)
-> Limit (cost=0.00..0.03 rows=1 width=8)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..33799.01 rows=1000000 width=8)
Filter: (value IS NOT NULL)
SubPlan 3
-> Limit (cost=0.22..0.26 rows=1 width=8)
InitPlan 2 (returns $3)
-> Limit (cost=0.18..0.22 rows=1 width=8)
InitPlan 1 (returns $2)
-> Limit (cost=0.02..0.18 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.02..17938.04 rows=111111 width=8)
Index Cond: (value <= (((floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)) + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)))
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $2)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..12104.70 rows=333333 width=8)
Index Cond: (value < ($3)[1])
SubPlan 7
-> Limit (cost=0.18..0.22 rows=1 width=8)
InitPlan 6 (returns $6)
-> Limit (cost=0.02..0.18 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.02..17938.04 rows=111111 width=8)
Index Cond: (value <= (((floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)) + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)))
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $6)
SubPlan 9
-> Limit (cost=0.18..0.22 rows=1 width=8)
InitPlan 8 (returns $7)
-> Limit (cost=0.02..0.18 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.02..17938.04 rows=111111 width=8)
Index Cond: (value <= (((floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)) + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)))
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $7)
-> WorkTable Scan on d (cost=0.04..6.31 rows=10 width=16)
Filter: (d.nextpiece IS NOT NULL)
InitPlan 15 (returns $13)
-> Result (cost=0.03..0.04 rows=1 width=0)
InitPlan 14 (returns $12)
-> Limit (cost=0.00..0.03 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..33799.01 rows=1000000 width=8)
Filter: (value IS NOT NULL)
SubPlan 13
-> Limit (cost=0.19..0.23 rows=1 width=8)
InitPlan 12 (returns $11)
-> Limit (cost=0.15..0.19 rows=1 width=8)
InitPlan 11 (returns $10)
-> Limit (cost=0.01..0.15 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..15438.04 rows=111111 width=8)
Index Cond: (value <= ((($9 + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= $9)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $10)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..12104.70 rows=333333 width=8)
Index Cond: (value < ($11)[1])
SubPlan 17
-> Limit (cost=0.15..0.19 rows=1 width=8)
InitPlan 16 (returns $14)
-> Limit (cost=0.01..0.15 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..15438.04 rows=111111 width=8)
Index Cond: (value <= ((($9 + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= $9)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $14)
SubPlan 19
-> Limit (cost=0.15..0.19 rows=1 width=8)
InitPlan 18 (returns $15)
-> Limit (cost=0.01..0.15 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..15438.04 rows=111111 width=8)
Index Cond: (value <= ((($9 + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= $9)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $15)
</pre>
</div>
Despite being huge in size, the query is very efficient and completes in only <strong>48 ms</strong>.
<h3>Locating values within the pieces</h3>
Now, when we have the exact bounds of each piece, we need to locate the records within each piece.
Since we don't have exact inverse function here, the basic idea is the same as above: given the approximate inverse, locate the exact bound using the iterative approach:
<ol>
<li>Locate the first key to the left of the inverse which yields the function result less than the one sought for, up to the first key of the piece. Should this search fail, the first key of the piece is the lower bound.</li>
<li>Locate the first key to the right of that found on the previous step that yields the function value equal to or greater than the one sought for, up to the last key of the piece. Return <code>NULL</code> should it fail</li>
</ol>
Since we have an inclusive range here, we don't need the third step (final scan to the left to find the rightmost least value) that we used when searching for the pieces.
This algorithm searches for the lower bound; to search for the upper bound, we just need to inverse both directions and tests (<q>left</q> becomes <q>right</q>, <q>less</q> becomes <q>greater</q> etc).
Since the monotony of the function varies from piece to piece, we should take this into account. For the pieces where the function's monotony is <code>DECREASING</code> we should swap the order of the bounds: the upper bound of the expression becomes the lower bound or the range of values and vice versa. This can be handled merely by substituting the conditions into the very same <code>CASE</code> expression that defines the monotony.
When we locate the upper and the lower bounds for each piece, we should just join <code>t_sine</code> on the following condition:
ON value BETWEEN llimit and ulimit
It can happen so that the lower bound found by the algorithm exceeds the upper bound. This is a perfectly normal situation meaning that no keys match the condition and the range diverged. BETWEEN predicate will handle this.
It also can happen that one of the bounds is a NULL. This is also a valid situation, meaning that no value within the piece exceeds the lower bound (or falls short of the upper one). BETWEEN will also take care of it.
Final query
And here's the final query. Be ready, you'll have to spin your mouse wheel a lot:
WITH RECURSIVE
d AS (
SELECT piece,
minv,
COALESCE(
(
SELECT value
FROM t_sine
WHERE value < nv[1]
ORDER BY
value DESC
LIMIT 1
),
(
SELECT MAX(value)
FROM t_sine
)
) AS maxv,
nv[1] AS nextv,
nv[2] AS nextpiece
FROM (
SELECT minv, piece,
(
SELECT ARRAY[value, FLOOR(value / PI() + 0.5)]
FROM t_sine
WHERE value >
(
SELECT value
FROM t_sine
WHERE value <= ((piece + 1) - 0.5) * PI()
AND FLOOR(value / PI() + 0.5) <= piece
ORDER BY
value DESC
LIMIT 1
)
ORDER BY
value
LIMIT 1
) nv
FROM (
SELECT minv, FLOOR(minv / PI() + 0.5) AS piece
FROM (
SELECT MIN(value) AS minv
FROM t_sine
) q
) q2
) q3
UNION ALL
SELECT piece,
minv,
COALESCE(
(
SELECT value
FROM t_sine
WHERE value < nv[1]
ORDER BY
value DESC
LIMIT 1
),
(
SELECT MAX(value)
FROM t_sine
)
) AS maxv,
nv[1] AS nextv,
nv[2] AS nextpiece
FROM (
SELECT minv, piece,
(
SELECT ARRAY[value, FLOOR(value / PI() + 0.5)]
FROM t_sine
WHERE value >
(
SELECT value
FROM t_sine
WHERE value <= ((piece + 1) - 0.5) * PI()
AND FLOOR(value / PI() + 0.5) <= piece
ORDER BY
value DESC
LIMIT 1
)
ORDER BY
value
LIMIT 1
) nv
FROM (
SELECT nextv AS minv, nextpiece AS piece
FROM d
WHERE nextpiece IS NOT NULL
) q2
) q3
)
SELECT l.*, s.*, SIN(value)
FROM (
SELECT minv, maxv,
CASE piece::INTEGER % 2
WHEN 0 THEN
(
SELECT value
FROM t_sine
WHERE value >=
COALESCE(
(
SELECT value
FROM t_sine
WHERE value <= LEAST(piece * PI() + ASIN(0.4452), maxv)
AND value >= minv
AND SIN(value) < 0.4452
ORDER BY
value DESC
LIMIT 1
),
minv
)
AND value <= maxv
AND SIN(value) >= 0.4452
ORDER BY
value
LIMIT 1
)
ELSE
(
SELECT value
FROM t_sine
WHERE value >=
COALESCE(
(
SELECT value
FROM t_sine
WHERE value <= LEAST(piece * PI() - ASIN(0.4453), maxv)
AND value >= minv
AND SIN(value) > 0.4453
ORDER BY
value DESC
LIMIT 1
),
minv
)
AND value <= maxv
AND SIN(value) <= 0.4453
ORDER BY
value
LIMIT 1
)
END AS llimit,
CASE piece::INTEGER % 2
WHEN 0 THEN
(
SELECT value
FROM t_sine
WHERE value <=
COALESCE(
(
SELECT value
FROM t_sine
WHERE value >= GREATEST(piece * PI() + ASIN(0.4453), minv)
AND value <= maxv
AND SIN(value) > 0.4453
ORDER BY
value
LIMIT 1
),
maxv
)
AND value >= minv
AND SIN(value) <= 0.4453
ORDER BY
value DESC
LIMIT 1
)
ELSE
(
SELECT value
FROM t_sine
WHERE value <=
COALESCE(
(
SELECT value
FROM t_sine
WHERE value >= GREATEST(piece * PI() - ASIN(0.4452), minv)
AND value <= maxv
AND SIN(value) < 0.4452
ORDER BY
value
LIMIT 1
),
maxv
)
AND value >= minv
AND SIN(value) >= 0.4452
ORDER BY
value DESC
LIMIT 1
)
END AS ulimit
FROM d
) l
JOIN t_sine s
ON value BETWEEN llimit AND ulimit
| minv | maxv | llimit | ulimit | id | value | sin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0172837972298265 | 1.57060804706216 | 0.46150185738802 | 0.46150185738802 | 3663 | 0.46150185738802 | 0.44529334884391 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.57081433883309 | 4.7123523916252 | 2.68013202354237 | 2.68015610060766 | 23783 | 2.68013202354237 | 0.445256434133825 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.57081433883309 | 4.7123523916252 | 2.68013202354237 | 2.68015610060766 | 19263 | 2.68015610060766 | 0.445234875325918 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.85409013534784 | 10.9955484666698 | 8.963312032599 | 8.963312032599 | 86110 | 8.963312032599 | 0.445261178083286 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10.9956333589859 | 14.1371444690436 | 13.0278523004308 | 13.0278523004308 | 128053 | 13.0278523004308 | 0.445275287664458 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14.1372372000463 | 17.2787474542275 | 15.2465362691633 | 15.2465362691633 | 150339 | 15.2465362691633 | 0.445226320346027 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17.2790936637506 | 20.4199075459354 | 19.310986539682 | 19.3110526885197 | 185849 | 19.310986539682 | 0.445229561181329 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17.2790936637506 | 20.4199075459354 | 19.310986539682 | 19.3110526885197 | 191391 | 19.3110088731334 | 0.445249558810258 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17.2790936637506 | 20.4199075459354 | 19.310986539682 | 19.3110526885197 | 186788 | 19.3110526885197 | 0.44528879096528 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20.4204805635758 | 23.561747650259 | 21.529697893659 | 21.5297331408583 | 212511 | 21.529697893659 | 0.445247526124325 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20.4204805635758 | 23.561747650259 | 21.529697893659 | 21.5297331408583 | 210841 | 21.5297331408583 | 0.445215965240229 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23.5619455649868 | 26.7032224601433 | 25.5941842560224 | 25.5941842560224 | 247639 | 25.5941842560224 | 0.445240672513922 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36.1283162861556 | 39.2698307414278 | 38.1605504324339 | 38.1606072025172 | 373019 | 38.1605504324339 | 0.445236698722671 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36.1283162861556 | 39.2698307414278 | 38.1605504324339 | 38.1606072025172 | 373416 | 38.1606072025172 | 0.445287530670759 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45.5530965244733 | 48.694549004443 | 46.6623900452435 | 46.662440645238 | 462683 | 46.6623900452435 | 0.445291469623201 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45.5530965244733 | 48.694549004443 | 46.6623900452435 | 46.662440645238 | 463233 | 46.6624209528782 | 0.445263795157205 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45.5530965244733 | 48.694549004443 | 46.6623900452435 | 46.662440645238 | 458141 | 46.6624391236514 | 0.445247524983561 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45.5530965244733 | 48.694549004443 | 46.6623900452435 | 46.662440645238 | 462704 | 46.662440645238 | 0.445246162542927 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51.8363581438176 | 54.9774493159346 | 52.945639446865 | 52.9456708737895 | 520118 | 52.945639446865 | 0.445234079463435 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51.8363581438176 | 54.9774493159346 | 52.945639446865 | 52.9456708737895 | 522686 | 52.9456708737895 | 0.445205939128705 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54.9779645633645 | 58.1193389566675 | 57.0100855686799 | 57.0100855686799 | 561721 | 57.0100855686799 | 0.445218087206929 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67.5442983367741 | 70.6858307610475 | 69.5764806582652 | 69.5764806582652 | 686886 | 69.5764806582652 | 0.445240002733585 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70.6861408688866 | 73.8273966856673 | 71.7951245983548 | 71.7952263388403 | 711952 | 71.7951245983548 | 0.445297446856164 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70.6861408688866 | 73.8273966856673 | 71.7951245983548 | 71.7952263388403 | 716508 | 71.7952263388403 | 0.445206347880861 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76.9690608614191 | 80.1104563690938 | 78.0783171531357 | 78.0783171531357 | 778116 | 78.0783171531357 | 0.445290957467673 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86.3938749629512 | 89.5353266705379 | 88.4260205388732 | 88.4260205388732 | 877138 | 88.4260205388732 | 0.445225639446173 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89.5354929595716 | 92.6769711233795 | 90.6446926224232 | 90.6446926224232 | 903050 | 90.6446926224232 | 0.445286610427917 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92.6770082124449 | 95.8184746547915 | 94.7092303088069 | 94.7092782433405 | 946181 | 94.7092303088069 | 0.445247543713327 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92.6770082124449 | 95.8184746547915 | 94.7092303088069 | 94.7092782433405 | 942345 | 94.7092782433405 | 0.44529046414363 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95.8185816861346 | 98.9601405610755 | 96.9279387165383 | 96.9279387165383 | 966815 | 96.9279387165383 | 0.445232181707114 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 98.9601765494391 | 100.992433886895 | 100.992433886895 | 100.992433886895 | 999931 | 100.992433886895 | 0.445263903548165 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 rows fetched in 0.0071s (0.1153s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nested Loop (cost=67.09..25557916.04 rows=11222222 width=36)
CTE d
-> Recursive Union (cost=0.08..65.97 rows=101 width=16)
-> Subquery Scan q (cost=0.08..0.80 rows=1 width=8)
InitPlan 5 (returns $5)
-> Result (cost=0.03..0.04 rows=1 width=0)
InitPlan 4 (returns $4)
-> Limit (cost=0.00..0.03 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..33799.01 rows=1000000 width=8)
Filter: (value IS NOT NULL)
-> Result (cost=0.03..0.04 rows=1 width=0)
InitPlan 10 (returns $8)
-> Limit (cost=0.00..0.03 rows=1 width=8)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..33799.01 rows=1000000 width=8)
Filter: (value IS NOT NULL)
SubPlan 3
-> Limit (cost=0.22..0.26 rows=1 width=8)
InitPlan 2 (returns $3)
-> Limit (cost=0.18..0.22 rows=1 width=8)
InitPlan 1 (returns $2)
-> Limit (cost=0.02..0.18 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.02..17938.04 rows=111111 width=8)
Index Cond: (value <= (((floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)) + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)))
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $2)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..12104.70 rows=333333 width=8)
Index Cond: (value < ($3)[1])
SubPlan 7
-> Limit (cost=0.18..0.22 rows=1 width=8)
InitPlan 6 (returns $6)
-> Limit (cost=0.02..0.18 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.02..17938.04 rows=111111 width=8)
Index Cond: (value <= (((floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)) + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)))
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $6)
SubPlan 9
-> Limit (cost=0.18..0.22 rows=1 width=8)
InitPlan 8 (returns $7)
-> Limit (cost=0.02..0.18 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.02..17938.04 rows=111111 width=8)
Index Cond: (value <= (((floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)) + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= floor((($1 / 3.14159265358979::double precision) + 0.5::double precision)))
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $7)
-> WorkTable Scan on d (cost=0.04..6.31 rows=10 width=16)
Filter: (d.nextpiece IS NOT NULL)
InitPlan 15 (returns $13)
-> Result (cost=0.03..0.04 rows=1 width=0)
InitPlan 14 (returns $12)
-> Limit (cost=0.00..0.03 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..33799.01 rows=1000000 width=8)
Filter: (value IS NOT NULL)
SubPlan 13
-> Limit (cost=0.19..0.23 rows=1 width=8)
InitPlan 12 (returns $11)
-> Limit (cost=0.15..0.19 rows=1 width=8)
InitPlan 11 (returns $10)
-> Limit (cost=0.01..0.15 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..15438.04 rows=111111 width=8)
Index Cond: (value <= ((($9 + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= $9)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $10)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..12104.70 rows=333333 width=8)
Index Cond: (value < ($11)[1])
SubPlan 17
-> Limit (cost=0.15..0.19 rows=1 width=8)
InitPlan 16 (returns $14)
-> Limit (cost=0.01..0.15 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..15438.04 rows=111111 width=8)
Index Cond: (value <= ((($9 + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= $9)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $14)
SubPlan 19
-> Limit (cost=0.15..0.19 rows=1 width=8)
InitPlan 18 (returns $15)
-> Limit (cost=0.01..0.15 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..15438.04 rows=111111 width=8)
Index Cond: (value <= ((($9 + 1::double precision) - 0.5::double precision) * 3.14159265358979::double precision))
Filter: (floor(((value / 3.14159265358979::double precision) + 0.5::double precision)) <= $9)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..14604.70 rows=333333 width=8)
Index Cond: (value > $15)
-> CTE Scan on d (cost=0.00..2.02 rows=101 width=24)
-> Index Scan using ix_sine_value on t_sine s (cost=1.12..2570.38 rows=111111 width=12)
Index Cond: ((s.value >= CASE ((d.piece)::integer % 2) WHEN 0 THEN (SubPlan 30) ELSE (SubPlan 32) END) AND (s.value <= CASE ((d.piece)::integer % 2) WHEN 0 THEN (SubPlan 34) ELSE (SubPlan 36) END))
SubPlan 30
-> Limit (cost=0.14..0.28 rows=1 width=8)
InitPlan 29 (returns $24)
-> Limit (cost=0.01..0.14 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..225.76 rows=1667 width=8)
Index Cond: ((value <= LEAST((($17 * 3.14159265358979::double precision) + 0.461397604523314::double precision), $18)) AND (value >= $19))
Filter: (sin(value) < 0.4452::double precision)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..225.75 rows=1667 width=8)
Index Cond: ((value >= COALESCE($24, $19)) AND (value <= $18))
Filter: (sin(value) >= 0.4452::double precision)
SubPlan 32
-> Limit (cost=0.14..0.28 rows=1 width=8)
InitPlan 31 (returns $25)
-> Limit (cost=0.01..0.14 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..225.76 rows=1667 width=8)
Index Cond: ((value <= LEAST((($17 * 3.14159265358979::double precision) - 0.461509285667814::double precision), $18)) AND (value >= $19))
Filter: (sin(value) > 0.4453::double precision)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..225.75 rows=1667 width=8)
Index Cond: ((value >= COALESCE($25, $19)) AND (value <= $18))
Filter: (sin(value) <= 0.4453::double precision)
SubPlan 34
-> Limit (cost=0.14..0.28 rows=1 width=8)
InitPlan 33 (returns $26)
-> Limit (cost=0.01..0.14 rows=1 width=8)
-> Index Scan using ix_sine_value on t_sine (cost=0.01..225.76 rows=1667 width=8)
Index Cond: ((value >= GREATEST((($17 * 3.14159265358979::double precision) + 0.461509285667814::double precision), $19)) AND (value <= $18))
Filter: (sin(value) > 0.4453::double precision)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..225.75 rows=1667 width=8)
Index Cond: ((value <= COALESCE($26, $18)) AND (value >= $19))
Filter: (sin(value) <= 0.4453::double precision)
SubPlan 36
-> Limit (cost=0.14..0.28 rows=1 width=8)
InitPlan 35 (returns $27)
-> Limit (cost=0.01..0.14 rows=1 width=8)
-> Index Scan using ix_sine_value on t_sine (cost=0.01..225.76 rows=1667 width=8)
Index Cond: ((value >= GREATEST((($17 * 3.14159265358979::double precision) - 0.461397604523314::double precision), $19)) AND (value <= $18))
Filter: (sin(value) < 0.4452::double precision)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..225.75 rows=1667 width=8)
Index Cond: ((value <= COALESCE($27, $18)) AND (value >= $19))
Filter: (sin(value) >= 0.4452::double precision)
SubPlan 22
-> Limit (cost=0.14..0.28 rows=1 width=8)
InitPlan 21 (returns $20)
-> Limit (cost=0.01..0.14 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..225.76 rows=1667 width=8)
Index Cond: ((value <= LEAST((($17 * 3.14159265358979::double precision) + 0.461397604523314::double precision), $18)) AND (value >= $19))
Filter: (sin(value) < 0.4452::double precision)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..225.75 rows=1667 width=8)
Index Cond: ((value >= COALESCE($20, $19)) AND (value <= $18))
Filter: (sin(value) >= 0.4452::double precision)
SubPlan 24
-> Limit (cost=0.14..0.28 rows=1 width=8)
InitPlan 23 (returns $21)
-> Limit (cost=0.01..0.14 rows=1 width=8)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.01..225.76 rows=1667 width=8)
Index Cond: ((value <= LEAST((($17 * 3.14159265358979::double precision) - 0.461509285667814::double precision), $18)) AND (value >= $19))
Filter: (sin(value) > 0.4453::double precision)
-> Index Scan using ix_sine_value on t_sine (cost=0.00..225.75 rows=1667 width=8)
Index Cond: ((value >= COALESCE($21, $19)) AND (value <= $18))
Filter: (sin(value) <= 0.4453::double precision)
SubPlan 26
-> Limit (cost=0.14..0.28 rows=1 width=8)
InitPlan 25 (returns $22)
-> Limit (cost=0.01..0.14 rows=1 width=8)
-> Index Scan using ix_sine_value on t_sine (cost=0.01..225.76 rows=1667 width=8)
Index Cond: ((value >= GREATEST((($17 * 3.14159265358979::double precision) + 0.461509285667814::double precision), $19)) AND (value <= $18))
Filter: (sin(value) > 0.4453::double precision)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..225.75 rows=1667 width=8)
Index Cond: ((value <= COALESCE($22, $18)) AND (value >= $19))
Filter: (sin(value) <= 0.4453::double precision)
SubPlan 28
-> Limit (cost=0.14..0.28 rows=1 width=8)
InitPlan 27 (returns $23)
-> Limit (cost=0.01..0.14 rows=1 width=8)
-> Index Scan using ix_sine_value on t_sine (cost=0.01..225.76 rows=1667 width=8)
Index Cond: ((value >= GREATEST((($17 * 3.14159265358979::double precision) - 0.461397604523314::double precision), $19)) AND (value <= $18))
Filter: (sin(value) < 0.4452::double precision)
-> Index Scan Backward using ix_sine_value on t_sine (cost=0.00..225.75 rows=1667 width=8)
Index Cond: ((value <= COALESCE($23, $18)) AND (value >= $19))
Filter: (sin(value) >= 0.4452::double precision)
This 200-line monster completes in only 110 ms, or 30 times as fast as the original 3-liner:
SELECT * FROM t_sine WHERE SIN(value) BETWEEN 0.1234 AND 0.1235
, yielding the same results.
Summary
This example was to demonstrate feasibility of the B-Tree indexes to be used in a search for the predicates involving monotonic functions and the performance gain achieved.
The performance gain is over 30 times for a table that fits completely into the cache, and will increase with the number of the cache misses increases.
The SQL implementation of the algorithm is in fact not optimal, since iterative searches for the value boundaries are implemented as the subqueries. Each subquery requires reentering the B-Tree and traversing it starting from the root. The native algorithm working within the optimizer could avoid this by caching the key position in the index and issuing next_key / prev_key commands, which would improve the algorithm yet more.
Sargability of the monotonic functions, as shown above, can help to make the queries like the one described in this article much more legible, maintainable and efficient.
Written by Quassnoi
February 23rd, 2010 at 11:00 pm
Posted in PostgreSQL
2 Responses to 'Sargability of monotonic functions: example'
Subscribe to comments with RSS
Leave a Reply
Subscribe
Subscribe by email
Contacts
Should I?
Yes. Feel free to ask questions and write me. An interesting question is a pleasure to answer, and I really enjoy receiving feedback
Recent articles
- Happy New Year: Diffusion Model image generator in about 700 lines of pure SQL
- Happy New Year: GPT in 500 lines of SQL
- Happy New Year: solving the Rubik’s Cube in SQL
- A good first word for Wordle
- Happy New Year: quantum computer emulator in SQL
Calendar
Archives
- December 2024
- December 2023
- December 2022
- January 2022
- December 2021
- December 2020
- December 2019
- December 2018
- December 2017
- December 2016
- December 2015
- December 2014
- July 2014
- December 2013
- October 2013
- September 2013
- August 2013
- July 2013
- June 2013
- May 2013
- March 2013
- January 2013
- December 2012
- December 2011
- June 2011
- April 2011
- March 2011
- February 2011
- December 2010
- November 2010
- October 2010
- September 2010
- August 2010
- July 2010
- June 2010
- May 2010
- April 2010
- March 2010
- February 2010
- January 2010
- December 2009
- November 2009
- October 2009
- September 2009
- August 2009
- July 2009
- June 2009
- May 2009
- April 2009
- March 2009
- February 2009
 Subscribe in a reader
Subscribe in a reader
Why not use functional index?
create index sin_idx on t_sin(sin(value));
satek
14 Oct 10 at 16:08
@satek: because this way you will need a separate index for each function you are going to filter on in your query.
The point is that you can filter on
sin(value), as well as any other monotonic function, using an index onvalue.Read the original article: https://explainextended.com/2010/02/19/things-sql-needs-sargability-of-monotonic-functions/
Quassnoi
14 Oct 10 at 16:33