Happy New Year: Diffusion Model image generator in about 700 lines of pure SQL
Regular readers of my blog will be aware that SQL is an excellent tool for graphics. You can use it to draw snowflakes, fractals, ray-traced 3D pictures, and many other things. SQL art is beautiful, albeit slow to generate.
These days they say AI is taking over, and human-made art will soon go the way of the dodo. The same fate awaits SQL-made art, I'm afraid. But you can't stop the progress. If you can't beat'em, join'em. To make regular art, you need regular AI, and to make SQL art, you need SQL AI.
So today, in an effort to save SQL art from extinction, we will be implementing a program capable of creating realistic images of butterflies from scratch—in SQL, of course.

As always, a little bit of theory first.
These days, most AI products that generate pictures (like Kandinsky, Stable Diffusion, Midjorney, and similar) are backed by variations of a technique known as Diffusion Model. I will try my best to explain the intuition behind it, while aiming to keep the level of math and formulas at the bare necessary minimum.
To illustrate the non-SQL related portions of this post, I'll be using a ready-to-use, pretrained model that I found on HuggingFace. This model is called gnokit/ddpm-butterflies-64.
It's a DDPM model, with the UNet architecture as a backbone, trained to perform denoising in 1000 steps with the linear noise schedule from 0.0001 to 0.02. I'll explain later what all these words mean.
It's been trained on the Smithsonian Butterflies dataset. It can unconditionally generate 64×64×3 images of butterflies that don't exist in nature. "Unconditionally" here means there is no prompt or anything. You just run it and get a random butterfly.
With that out of the way, let's begin. First of all, what the hell is DDPM?
The Denoising Diffusion Probabilistic Model
There is a popular quote attributed to Michelangelo. When asked about how he made his statues, he responded: "I saw the angel trapped in the marble and I carved until I set him free". Translated to the language of math, it means that he saw a block of marble in front of him, the angel's image in his mind, and was able to calculate, so to speak, their difference: how much marble he should have chiseled away at any given place until the former became the latter.
Just like this:

Making statues and painting pictures is something Michelangelo could do, and I can't. But this never stopped me from giving advice. Everything I can do, I do by making a series of small, simple steps, each one bringing my work closer to the completion. When you learn a craft, you have to learn two things: first, what do to on every one of the small, simple steps; second, which step leads to which next one.
Learning how to make art (or anything else, for that matter) works the same way: break everything into many small pieces, and learn how to complete every piece. When you see Bob Ross painting lessons on TV, it's a series of simple brush strokes, going from a half-incomplete picture to a slightly less incomplete one.
Turns out, computers can learn how to paint in the same way.
When you teach a computer how to paint, you show it pairs of images of stuff. The first image in the pair is the original photo, and the second one is the same photo with some noise added. The amount of noise varies from very little (almost clear picture) to very large (almost completely random pixels). You also tell the computer how much noise you have added.
During the training phase, the computer gets lots of these pairs and feeds them into the special function. This function is called the "backbone" of the model (or, quite often, just the "model").
On input, the function receives two values: a vector with the pixels of the dirty image, and the amount of noise (a scalar number).
On output, it returns an image that is supposed to be as close to the original image as possible. Or, what is essentially the same, the vector with the noise that you need to subtract from the dirty image to get back to the original.
The output of the function needs to have the same shape as the input. If the first input parameter to the function is a 64 (height) × 64 (width) × 3 (RGB) vector that represents a dirty image, so is the function output, which represents the noise it "thinks" was added to the original.
Here's the shape of the function:
backbone(image: vector, step: int) -> vector # Takes the dirty image and the amount of noise added to it. The amount of noise is encoded in an integer # Returns the noise
The function doesn't receive the original image. It has to guess what it was just from the dirty image, and the amount of noise. Note that the amount of noise is encoded as an integer (I'll explain later why)
How does the backbone predict the noise?
The backbone function is composed of a series of simple operations. These operations are matrix multiplications and additions (lots of them), exponentiations, logarithms, and simple trig. All these operations (and, hence, their composition) are differentiable.
The matrix multiplications that happen inside the functions use a lot of constants that are baked into the function (i.e. don't come from its inputs). During the training phase, these constants can change between invocations — and changing them is exactly what training does —but once the training is done, these constants are set in stone. They are called "parameters" of the model. Their values can change (only during the training), but their total number and shapes (whether they are scalars, vectors, or matrices) are set at design time. All of this together: the code of the function, and the shapes of its internal parameters, is called the "architecture" of the model.
Before the training commences, these parameters are set to random values (literally, random). On the first invocation, the function, of course, does a very poor job of predicting the added noise. The training process looks at its output (rather underwhelming, at first) and compares it to the real vector of noise that has been added. Unlike the backbone, the training process knows both the original image and the added noise.
"Comparing" noises, in this case, means calling a special function called the "loss function". The loss function returns a single number (a scalar). The smaller the difference between the predicted and the actual noise vectors, the lower the return value of the loss function, with 0 meaning the ideal match.
The exact shape of the loss function is not an integral part of the backbone (it's only being used during the training phase). The authors of the original DDPM paper found out that Mean Squared Error (the sum of squares of the differences between predicted and actual noise values for each pixel and channel) works quite well as a loss function.
Once the first pass of the function has been performed and the loss value has been calculated, the actual learning process happens.
As a developer, you compose your backbone function by chaining methods from your framework (take this vector; multiply it by this matrix of weight constants; add a vector of bias constants; take the exponent, and so on).
The framework that is doing the training tracks all the operations that the function performs, records their order, and calculates the partial derivatives with respect to all the parameters that were used in this function. It uses the technique known as automatic differentiation. Most popular frameworks used for machine learning (PyTorch, TensorFlow and others) have built-in utilities that let the developer just compose the functions, and the framework will take care of the differentiation.
The return value of the loss function, at a cursory glance, looks like a single scalar number. But the variable where it's stored also carries an auxiliary data structure for the framework's internal use. This structure keeps the whole graph of the calculations performed on the inputs and the parameters, which eventually led to the number. It also stores cached numeric values of the gradient of the loss function, or, in other words, the value of its partial derivatives with respect to all the parameters that have been part of this graph. The parameters in a DDPM usually number in the millions or even billions. One puny number carries the whole history of how this number came to be.
The loss function is also tracked by the automatic differentiation framework. It means it has to be differentiable (and simple enough) as well. The calculation of the loss is composed of those of the backbone (which is differentiable), and those of the mean squared error (which is differentiable too). Making a small enough change to the parameters results in a small change in the value of the loss function. So what happens if we change the values of all the parameters in the direction opposite that of the gradient? The value of the loss will, quite mechanically, become smaller, which is what we want.
Once the loss has been calculated, the framework looks at the gradient of the loss function, and adjusts all the parameters ever so slightly opposite the gradient. It does it so that the backbone, had it been called again with the same input and new parameters, would return a smaller loss. This process is called backpropagation.
Note that I said that the loss would be smaller for the same input. But the inputs don't repeat during the real training. On every step, the loss function is fixed to work better with the old data, but doesn't get to enjoy it: on the next step, it will get new data. The results will still be underwhelming, but this time, hopefully, less so.
This process is repeated until the loss function settles on its minimum. It's not guaranteed to happen, though:
- The loss, after a certain number of steps, might stop decreasing and start growing. It happens when the model becomes so good at reproducing the pictures from its initial training data, that it can't learn how to paint anything else. This is called overfitting.
- The training process takes a long time and we run out of money to rent GPUs.
- Finally, we might have picked the wrong math for our function. If that's the case, we can keep training it until the cows come home, and it still won't converge to an acceptable level of loss.
But if we manage to come up with a good model architecture (i.e. we are composing just the right sequence of linear algebra, exponents, and trig), the model will converge fast on a small enough loss value. It means it can take a noisy picture of a butterfly, and predict how to undo the noise quite well.
Why is it called "diffusion"?
The name comes from the similarly named concept in physics. If you carefully put a drop of red dye in water, the dye will start diffusing. The molecules of the dye will become subject to the Brownian motion (also known as random walk). The drop will keep its original round shape for a brief moment, then it will become slightly less round, then a formless cloud, and so on, until all the traces of the original shape are lost and water would acquire a uniform pinkish color. It's a gradual process. Each blurry shape of the dye cloud comes from a less blurry one that was there a moment ago, by adding a little bit of chaos to it. This process is known as the Markov chain.
The original idea of adding the noise to the clear image was similar to that. The noise would be added gradually, in small increments, through a Markov chain. Each subsequent noisy image would have a dependency on the previous, slightly less noisy one. The model would learn to undo the noise added on each step.
How many steps should be there and how much noise should we add on each step? It's up to the developer. We could add the same amount of noise, or make it grow linearly, or even come up with a function. The authors of the original DDPM paper decided to use 1000 steps, and make the amount of noise grow linearly with each step: from 0.0001 on the first step (least noisy image) to 0.02 on the last one (most noisy).
"Adding" is a little bit of a misnomer here: as we are sequentially "adding" amounts of noise, we are actually multiplying one's complements of these amounts (what's left of the original image). If we do the math, we'll see that on step 1000 the share of the original image will be about 4e-05. At this point, we can safely ignore it and say that the 1000's step on this Markov's chain is indistinguishable from noise.
These figures: the total number of steps, and the amounts of noise added on each step, are called the "noise schedule" of the model. If you remember, our backbone function accepts the noise level encoded in an integer. This integer is just the number of the step on the Markov chain. From this number, and from the noise schedule, we can always figure out the exact amount of noise.
This sounds promising in theory, but let's recall how training works. The model takes the noisy image on input and returns its best estimation of the non-noisy image on the output. If we added noise to the images in small increments, we would have to give the model every intermediate image during the training phase.
It means that to train the model to undo small amounts of noise added 250 times over (which, the way the math works, would result in about 50% noise in total), we would have to run 250 passes over 250 images, each one having just a tiny bit of noise added to the image from the previous step.
This is bad for several reasons:
- It's very expensive computationally.
- With that much math, there's a good chance that rounding errors will pile up to the point where all the original signal drowns in rounding errors.
-
It has to do with how the automatic differentiation works well towards decreasing the loss function. It needs to track the path of the original input to the model (which is taken for granted) through the math operations over the constants ("parameters"). The constants are being adjusted along their gradients and, once the learning is done with, are set in stone.
Noise is not the parameters, so it has to be the input. We will have 700 instances of noise added to one single instance of the original image. Since to the model, all the numbers are the same and their "meaning" only emerges, if ever, during the training phase, it will have a much harder time discerning the original image from all that noise.
- The sequence of the functions inside the model will now explicitly depend on its input. While models can have loops over the same parameters inside of them, the number of iterations in these loops has to be fixed at design time. This particular problem can be fixed by hardcoding the number of the loops to 1000 and substituting missing images with zeros or something, but then again, it will take more time.
With all this, it seems like the Markov chain approach isn't exactly going to work out of the box. But the authors of the original DDPM architecture have made a very astute observation that allowed them to fix it and save the day.
Reparameterization
If you generate noise just by putting a random value sampled from the Gaussian distribution (with the mean 0 and the variance 1) to every pixel of the noise vector, the end result will also come out as if sampled from the standard Gaussian distribution
, with 0 for the mean and identity for the covariation matrix. The Gaussian distribution is also known as the normal distribution, or the bell curve distribution.
Now, you have two options for generating a dirty image. You can go by the book and add a certain small amount of standard Gaussian noise to the image in many sequential steps. Or you can make a shortcut of sorts. You can take the same image, sample the noise just once, and add a bigger amount of that noise to the clean image in one fell swoop, this bigger amount being defined by a simple enough formula.
One nice property of the standard bell curve noise is that the end results of both these operations will be identical from the statistical point of view. They will have the same distribution. It means that the results of both these operations, repeated many times over, will look like equally noisy images of butterflies or whatever it was in the training set. There's no way to tell the results of these two processes apart using statistical methods. If the result of the sequential process was good enough to usefully train the model, so will be the result of the shortcut process.
From the math perspective, adding an amount of noise to the vector of image pixel intensities twice looks like this:
Here, and
are two different random variables sampled from the same standard Gaussian distribution. The expression in the square brackets is a sum of two independent, normally distributed variables, and can be replaced with another random variable. It will also be normally distributed, with a mean equal to the sum of the terms' means, and the variance equal to the sum of terms' variances. The means are zero and will remain so. Variances depend on the scale, so those will change. We can replace the expression in the brackets:
and the final result for the image with noise added twice will look like this:
It's easy to see that the formula for every next step will be exactly the same, just with more factors in the product. So instead of adding a certain amount of noise step by step, you can calculate the total amount of noise using the formula above, and add it all at once. The results will be statistically indistinguishable.
This technique is known as the reparameterization trick. In hindsight, it might look like a simple, even an obvious thing. But it took a great bit of ingenuity to notice it and put it to work.
In practice, it means that you don't have to go through all the steps to generate an image with a bigger amount of noise, and don't have to feed the intermediate results to the model either. You can just feed the number of steps to the formula and find the right amount of noise at once.
Another nice effect of this trick is that if you generate an image on step from a Gaussian sample, you can use the same sample to generate an image on step
. The difference between these two images (that is, the noise that would have been added on step
) would also have the same standard Gaussian distribution, whose parameters are easily calculatable.
We can pretend to have a Markov chain without actually computing all of its steps.
Where are the small steps?
Putting all the above together, we have a model that takes a noisy image and the amount of noise added to it and does a semi-decent job of predicting what the original image would be.
The model can now, so to say, see the images trapped inside white noise and set them free.
I can hear the model saying: "I see a piece of marble, and you say that the angel is about halfway inside. This is good enough. I see the vague shape of the wings, face, and everything else. I know a thing or two about angels. I have a good idea of how much marble I need to chisel away at every point to set the angel free. Give me a chisel and a mallet, and step aside".
Now, we've trained the model to work separately with each step, including those close to the end. As we remember, at step 1000 the dirty image is virtually indistinguishable from white noise. By the end of the training process, the loss level is supposed to be small and uniform, regardless of the step (if that's not the case, we don't have a good model to begin with). The model should do a decent enough job of reconstructing the original image from any step.
So, technically, we don't even need to begin with an image that once was a butterfly. We can just give the model chemically pure white noise. Then we would tell it to work its way back from step 1000, and it would paint us a butterfly.
Right?
Well, let's see how it works in practice.
We'll take the backbone function of the trained model, feed it some noise, and ask it to reconstruct the image from step 1000.
Here's what we get:

Is it a butterfly?
Well, it's definitely… something. It's not white noise. If you squint hard enough, you can see some kind of pattern, a very vague outline of the wings. But even its own grandmother wouldn't call it a butterfly.
So the model made a prediction about how to cancel the noise all the way through to the original image. The results of this prediction don't look good. Maybe we didn't need to go all the way through at once? After all, why did we learn on all these different noise levels separately?
Now, it looks like it's time for a little heart-to-heart with the model.
Listen, Michelangelo. I know you mean well. You think you know exactly how to set the angel free. Remove the noise all the way to what you think is the butterfly. Let me be straight with you: you can't. But hear me out now.
What if you didn't try to do this all at once? Instead of chiseling away all this noise, how about you just start in the right direction but don't work all your way through?
You're at step 1000 now. Don't go right to zero. Start removing the noise, but stop at the same amount step 999 would have. It would still be mostly noise, but this time a little bit closer to the butterfly. Then just run the backbone again with the new data, see if the noise estimation will correct itself a little bit, and then we maybe will do a better job next time.
How about that, buddy? Baby steps, remember.
Ah, it's a computer, it doesn't understand what we say anyway. So we will explain it in pseudocode:
# Algorithm to generate an image using the Denoising Diffusion Probabilistic Model:
image = random(height, width, channels) # -> vector Random pixels
for step in reverse(range(0, 1000, -1)): # from 999 to 0
noise = backbone(image: vector, step: int) # Predict noise
image = subtract_some_noise(image, noise, step) # Subtract predicted noise
image = image + add_noise(step) if step > 0 else 0 # Add some noise (yes, add). More on that later
return image # 0% noise, realistic photo
And this is how you get the baby steps. And most AI image generation software actually works this way. "Knowing" how pictures become noise, it starts from pure noise and tries to gradually cancel it to get a picture. This noise was not generated from the Markov chain and had never been added to a picture in the first place. But the model still tries to gradually cancel it in steps. And, in so doing, arrive at the picture that this noise would have been added to, had it existed in reality.
Crazy as it sounds, it works.
Backbone
There are several popular architectures for the backbone of the model, the function that is doing the heavy lift. The one that the butterfly model is using is called U-Net. We'll go through its internals in a short while. But first, let's look at some general principles.
Where do we start with the backbone at all?
In the Middle Ages, there were artists who knew elephants existed but never saw them. They made their artistic impressions of elephants from their verbal descriptions. Here are some of them:



A verbal description of an elephant resembles a grocery list of its characteristic features: "long trunk with bell mouth at the end," "big ears," "tusks," and so on. It's somewhat of a vector. You check every dimension, you get yourself an elephant. The animals in the pictures above fit these descriptions. We can recognize them as elephants, albeit funny-looking ones. What is it exactly that is so funny about them?
The grocery lists off of which the artists worked were incomplete. They did mention big ears and long trunks, but omitted the shapes of the legs, the body proportions, and other important things. The artists were applying these features on top of the images of the animals that had already existed in their minds. The beasts in the pictures are, essentially, goats and lions, whose ears were made bigger and noses longer as to match the incomplete description. This, however, was enough to make us see what they meant.
The working hypothesis is that if we somehow make a complete list of all the features of an elephant, or a butterfly, or anything else, we can make a photo-realistic picture of it. How do we go about it?
Latent space
Generative AI models work with images of certain fixed dimensions. When we see, say, a 64 × 64 × 3 image (height, width, and colors), we can treat it as a vector with 12288 dimensions. Every dimension of this vector will represent the brightness of a certain pixel. For simplicity, we'll assume that the values are from 0 (black) to 1 (the brightest color your monitor can handle).
We need a function that would map this vector to a vector of "butterflyness," so to speak, the grocery list of all things that, taken together, make a butterfly. It's, supposedly, quite a long list. If maybe one or two things are missing from it, it would be a "funny butterfly," or maybe a "cartoon butterfly," but still a butterfly alright. The items on this list should be encoded with continuous numbers, and the mapping should be differentiable.
The space of such vectors would be called a "latent space."
The main idea behind machine learning is that humans are not even supposed to try to describe these features analytically. The mapping would, as they put it, "emerge" during the training phase, the basic mechanics of which we learned in the previous section.
A quick refresher. The most common way of mapping one vector to another is the linear mapping. Mathematically, it's a matrix multiplication (by a matrix of constants) that changes the dimensions, followed by a vector addition (with a constant term) that translates the result. The constants in the factor matrix are traditionally called weights, and the constants in the summand vector are traditionally called biases. The linear mapping is a differentiable operation that lends itself easily to the procedure of machine learning.
You can stack linear mappings, but however many you stack, the end result will still be a linear mapping, which can be reformulated with a single matrix of weights and a single vector of biases, so stacking them makes no real difference.
Very soon people understood that linear mappings are a powerful, but not omnipotent, tool and have one very nasty limitation.
Vectors live in linear spaces, and every linear space can be cut in half by a hyperplane. A 2D space can be cut in half by a line, a 3D space by a plane, and so on. Turns out that if the feature vector that you're trying to learn is linearly inseparable, that is, you can't draw a straight line, or a plane, or a hyperplane in such a way that all the "butterflies" would stay on one side of it and all "non-butterflies" on the other, then linear mappings wouldn't work.
However, if you combine as few as two linear mappings, putting a non-linear function after each one of them, then, at least in theory, this combination can model just about everything we care about. The only limitation is the number of the dimensions in the vector space. You might be able to model any function, but you might need vectors with one million, or one billion, or any other number of dimensions for that. You might be more successful if you stack more than one linear mapping, interspersing them with non-linear functions (called "activators," or "activation functions," in machine learning parlance). Of course, the activation function should be differentiable as well.
Such a sandwich of linear mappings and activators is called a "neural network." A linear mapping plus activation is called a "layer." It's a basic building unit of almost all things AI. Everything is done by stacking layers of linear mappings and activation functions in clever ways.
Our intuition is to make two stacks of NN layers. The first stack would map the pixels of the image into a vector in the latent space. Some dimensions of this vector would be features that make a butterfly a butterfly (whatever it might be), and the rest of the dimensions would be responsible for everything else. The second stack would bump the butterfly-related components of the vector all the way up to eleven, to the Platonic ideal of butterflyness, leaving everything else as is or not even caring about it, and then map the result back to the image. This would make it the original image, just without noise. The difference would be noise, and we would return it to the loop that cancels the noise (it's called the schedule runner).
Again, that's just general intuition. We don't know what the "latent space of butterflyness" looks like or will look like, we don't know what its components do or will represent. We can't (generally) come up with them on purpose, or isolate their meanings in human-understandable terms.
All we can do is give the neural network enough dimensions to work with and use whatever little intuition we have in connecting these dimensions the way that we hope will help it converge. The exact semantics of all these features, dimensions, and latent spaces will emerge when (and if) the training converges on a small enough value of the loss function, and we still won't know what they are and how exactly they work.
Sounds promising, ain't it?
How do I design all these neural stacks?
Is it a general question? If yes, I'm sorry, I don't know. Really. Sorry.
The answer to this question would be the same as to "How do I compose a melody?" or "How do I write a short story?": simple, but utterly useless. Here it is. You write stories by putting the letters in order, left to right, minding your commas. You compose a melody by stacking lenghts of chords and pauses between them. They have to make sense, be captivating, and be pleasant to the eye or the ear. The same thing about machine learning. It has to be computationally feasible; it has to converge at the end of the training phase; and it has to do its job. That's it. It's an art. I don't know how to do that.
However, same as with composing and creative writing, there's a talent component to it, and there's a craft component to it. Inspiration and perspiration, and all this jazz. As for the craft part, there are some tricks and patterns that have empirically proven to be useful over the years. We'll now consider some of these tricks.
Convolution
It's a special kind of NN layer, particularly useful when working with images.
The input and the output vectors are laid out as 2D grids (or, in other words, matrices). Each pixel of the output vector is computed by a Frobenius inner product of the input matrix and some constant parameters—not of the whole input vector, though, but of its smaller sliding subgrid. In machine learning parlance, it is said that this layer is not fully connected, because not every component of the input vector affects every component of the output vector.
Mathematically, it's equivalent to a fully connected layer with some constants hardcoded to be 0 and not change during the training phase.
Convolution is particularly useful for isolating different features of images, and convolutions are being used in graphics processing even outside the domain of machine learning. When you open your favorite graphics editor and do things like blurring, sharpening, edge detection, magic wand selection, and so on, under the hood it runs convolutions.
This page has a nice interactive demonstration of convolutions and how you can use them in image processing. The parameters in the matrix multiplied with the sliding window are learned during the training phase, but its shape and dimensions are fixed at design time.
Having these layers instead of fully connected layers helps the model to isolate visual features while bringing down the amount of number crunching.
Residual connections
We make a fully connected layer (or several layers), and then, in a separate operation, we add its input to the output.
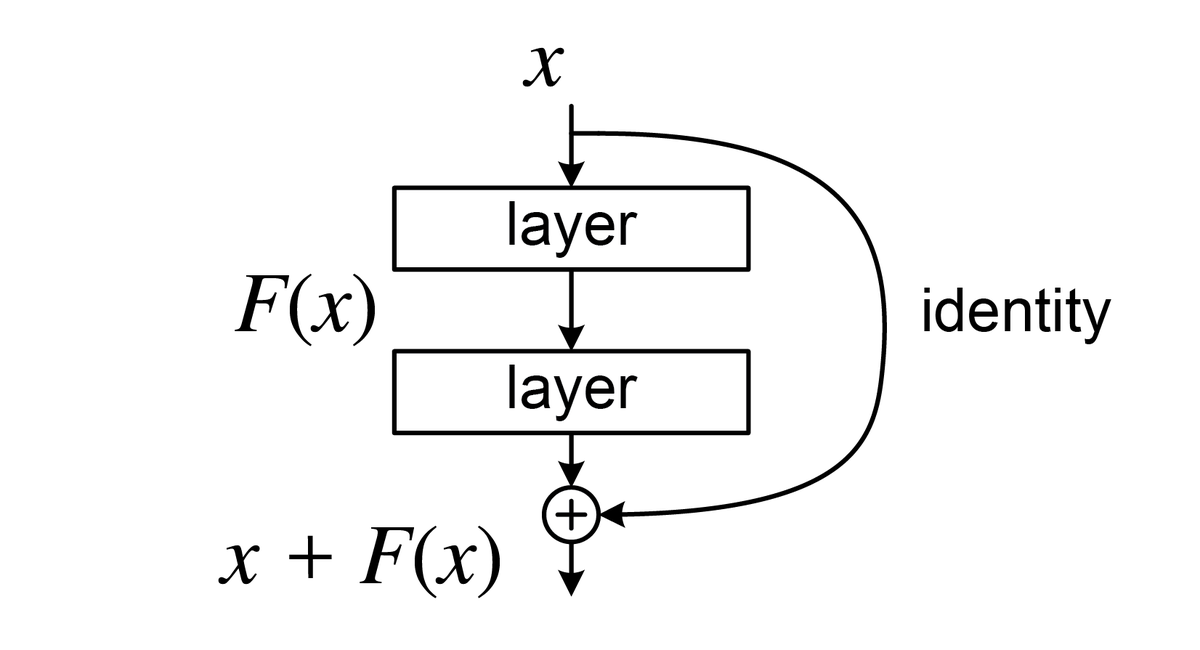
Before that, our neural network looked like a sandwich, and now it looks more like a taco. Mathematically, this operation is equivalent to adding a hidden layer with hardcoded 0's and 1's at certain places in weights and biases, and the identity function for the activator, so it's still a sandwich, i.e. a good old stack of linear maps and activations. Still, it's much easier to reason about it this way.
This method has been empirically found to help with exploding and vanishing gradients. If the neural model comprises a lot of stacked layers, its partial derivatives in respect to individual parameters may become either very small or very large. If it happens, the model as a whole becomes either too little sensitive to parameter changes (and, thus, never converges) or too sensitive, in which case even a small change to the parameter value throws the loss function too far away from a local minimum. Adding residual connections inside the network helps with that problem.
Normalization
Most neural networks start their training being initialized to random numbers. During the training itself, features emerge, and they are being encoded with different dimensions inside the latent spaces. But in the beginning, it's just a goo of numbers, like in a pupa from which a butterfly would then emerge (see what I did here?). All these numbers have the same distribution, and their numerical values are on the same scale.
If these numbers happen to encode different features and will come to live in different dimensions, some of these numbers might happen to become higher, and some lower. Household values of mass are measured in the range of 10e-3 through 10e3 kilograms, those of time in the range of 1 through 10e8 seconds, and those of, I don't know, electric capacitance in the range of 10e-15 through 10e-6 farad. It's been noted (again, empirically) that models that happen to keep their parameters in the same range train better and converge faster. We humans have the same problem; that's why we have invented all these "kilo-," "mega-," "micro-," and other prefixes that help us keep our numbers in palatable ranges.
Because of this, it helps if, every now and then, there are layers whose only purpose in life is bringing the numbers flowing through all the math to the same general range. They are just being multiplied by a certain number: usually, the reciprocal of their average, root mean, or something like this. It can be done for all the numbers in the network or separately for different chunks of them. Different techniques for that are called "layer normalization," "instance normalization," "group normalization," etc. (see Group Normalization, Wu, He, arXiv:1803.08494), which are different implementations of the same general idea.
Attention
This layer is generally considered one of the most (if not the most) important things that have contributed into the AI boom of today. It's been introduced in the famous paper Attention Is All You Need, Vaswani et al., arXiv:1706.03762.
The intuition behind this layer is that it splits a hidden layer into several subvectors and tries to encode the level of influence each pair of the subvectors exerts on each other. The assumption is that if we model the function this way, it will help the model understand how different features (that will emerge during the training and of which we don't know in advance) correlate with each other. It's supposed to mimic the way attention in humans and other animals works.
The values of correlations are taken from something known as a "differentiable key-value store." It's not a real key-value store; it's just a catchy name for a particular way to connect vectors in a neural network. Here's the intuition behind it, the way I understand it.
Let's consider a regular key-value store, where both keys and values are floating-point numbers and cannot be null. The store returns the stored value () if the query (
) equals the key (
). If not, it returns 0, for the lack of a magic value signifying a miss. It can be modeled by the expression
, where
is the Kronecker delta function.
The Kronecker delta is not a differentiable function and cannot be directly used in the neural network, so we have to approximate it using differentiable functions. A good enough approximation of the Kronecker delta is our good friend, the normal distribution, scaled to , with the mean around
and low enough variance. If
is "close enough" to
, then the expression will evaluate to a value "close enough" to
, and to zero otherwise.
and
are vectors, and in vector spaces, "close" means "has large cosine similarity." The cosine similarity is the value of the dot product of two vectors, scaled down to the range of
. So the expression for the "differentiable key-value store" would become
, which then gets scaled down. The exact nature of the downscaling process varies between implementations, but usually, the softmax function is being used for that.
The values of keys, values, and queries are not learned parameters (or, rather, not just learned parameters). They change their values on every invocation (or, the way they usually put it, "forward pass") of the neural network even outside the training phase. This is the closest thing that the neural network has to short-term memory.
Now that we are done with the basics, let's move to higher-level building blocks.
U-Net
Here's the diagram of the U-Net architecture:
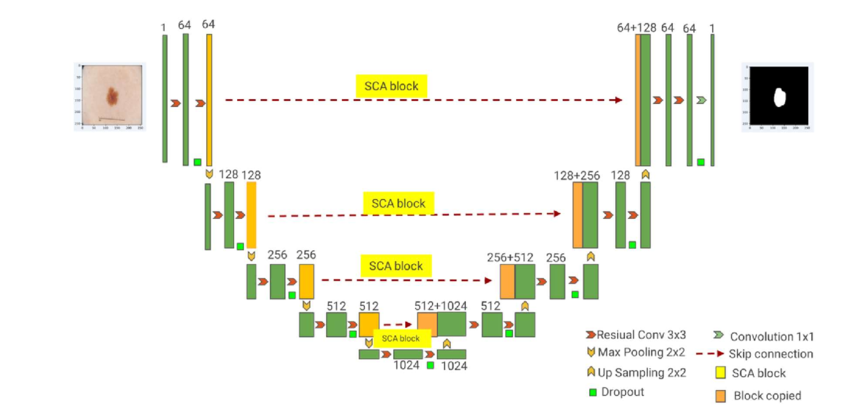
DOI: 10.3934/mbe.2023485
This architecture consists of three pieces:
- The encoder (the left-hand side of the U), which maps the image from a vector of RGB pixels to a vector in the latent space.
- The middle part, which runs attention and residual connections on the latent space
- The decoder (the right-hand side of the U), which maps the vector in the latent space to the vector of noise pixels in RGB.
The left-hand and the right-hand sides of the U are traditionally being called "encoder" and "decoder," but it's a little bit of a misnomer, because they have residual connections bypassing the latent space layer. A pure encoder and a pure decoder would have been able to work independently of each other, only communicating through the latent space.
The backbone of the model that we are exploring looks almost like the one on the diagram, with a couple of differences (which I will mention separately). Here's what's going on in the implementation of the U-Net architecture that drives the model:
- On the encoder, there are four big submodels. Each one of them comprises two blocks known as ResNets.
- Every ResNet consists of two convolutional layers (with a 3×3 kernel) and a residual connection. The activation function is the sigmoid.
- Before the convolutional layers, the image is group-normalized with 32 groups.
- After the first convolutional layer, the image is mixed with a vector encoding information about the current noise schedule step (more about that later).
- The image starts out with three channels (RGB) and not one, as in the picture. In every one of the four decoder's blocks, it's split into more channels (64, 128, 256, and 512, accordingly), and later, the channels are recombined in the encoder's blocks.
- After each ResNet, a downsampling is performed. Instead of using Max Pooling (like in the picture), our model uses strided convolution. It works like a regular convolution, but the sliding subgrid moves two cells at a time across the grid. The output grid, as it is easy to see, comes out twice as small.
- In the bottom two blocks on the left side of the U, after each ResNet, an attention block is added (not shown on the picture).
- The bottom side of the U is where the heavy lifting is happening. It's two ResNets in a sequence, with an attention block between them. The working theory is that at this layer, our vectors are in the latent space and record different aspects of the butterflyness of the original image more or less orthogonally in their dimensions.
- The right side of the U (the decoder) mirrors the left side, but with a little twist: inputs and outputs are twice as large, and there are three ResNets instead of two. It's because for the encoder, we concatenate the results from the bottom layer with the results that came straight from the appropriate parts of the decoder. This is sort of a residual layer on steroids, and its presence has been shown to help with the stability of the training process.
- There is also an attention block between the two ResNets in the middle part. (Attention blocks are not shown on the diagram.)
Step encoding
We remember that our backbone receives two parameters: the image itself and the number of step in the noise schedule. Where does the step number go?
Theoretically, we could have just multiplied the original image by it or added it. However, those would have been linear operations, and those get lost really easily during training (the first normalization block on the way would have killed them both). We need some way to make it more robust and, ideally, spread it along more dimensions so that more parameters would be influenced by its value.
How do we go about it?
A single number from 0 to 999 can be encoded with a 10-bit value that easily fits into a single floating-point variable and even leaves some extra space. For the most use scenarios, that would be fine. Usually, people try to pack as much data as possible into a single variable. That's what compression algorithms are for.
But now, for a change, we need to solve the opposite task: how to encode this value using a lot of variables? The more, the merrier. Our input vectors have the number 64 among their dimensions, so different values of 64 float variables would be a good start. And remember, no cheating. No stuffing with zeros or something like that. All these variables have to be different and meaningful; otherwise they will get cancelled by the first normalization block or bias vector on the way.
One thing we can do is make each digit go into a separate dimension, so, say, for step 576, 5 would go to the first dimension of the vector, 7 into the second one, and 6 into the third one. Three dimensions covered, sixty-one more to go. Can we do better?
Well, we can do the binary. 999 is 1111100111 in binary; that's 10 bits, so ten dimensions are covered, fifty-four more to go. And this, mind you, is not a good encoding for neural network purposes. Ones and zeros are way too discrete; we like things that are more smooth and differentiable. Can we do better?
It might be hard to see how we can go to a base less than binary (?), while making it less discrete (???), but amazingly enough, there is a way.
Let's look at binary encodings of some integer numbers, starting from zero:
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1 0 1
0 0 0 0 0 0 0 1 1 0
0 0 0 0 0 0 0 1 1 1
0 0 0 0 0 0 1 0 0 0
etc.
We can see that the last digit changes with every number, the one before last every two numbers, the one before it every four numbers, and so on. Every number has a very strict and regular periodic pattern.
What else has a periodic pattern? Why, the trigonometric functions have. We could represent any natural number using this expression:
and then use terms of this expression for the components of the vector (ditching the factors). This would boil down to just using 0s and 1s of the binary representation, so we would have run out of 1s by the eleventh dimension.
But let's look closer at this expression. We want to get rid of discreteness and make everything smooth, right? And we want to have meaningful numbers?
The first thing we could do is get rid of that ceiling operation inside the argument to the cosine. This would kill the exact mapping to the original number. But we don't need the number's exact value; we just need it encoded in a vector. The exact number would actually only confuse the neural network.
And while we're at that, let's look at the denominators inside the argument to the cosine. They are 1, 2, 4, 8, and so on, so the powers of two. Two is the smallest natural number that has meaningful powers, but now that we don't care about natural anymore, why can't we go lower than two but higher than one? Real numbers would work just as well for the base, and this way we would have more meaningful digits.
This is exactly how the encoding of the step numbers works. Here's the expression for it:
Here's what some of the dimensions of this vector look like for the first 100 timesteps:
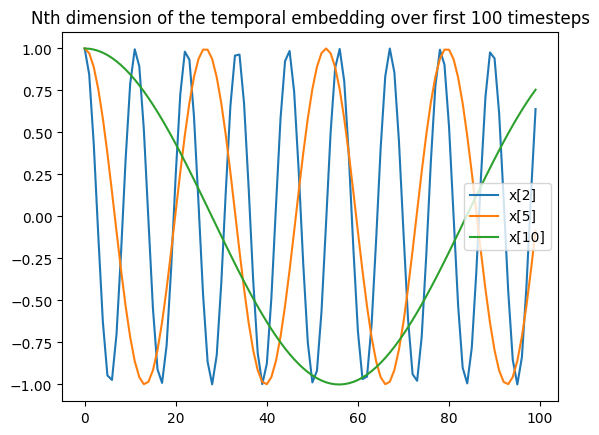
All the numbers are smooth, periodic, and all of them make good use of the dimensions space.
This technique is known as sinusoidal position embedding, and is closely related to the Fourier Transform, an enormously useful technique for just about any field of signal processing.
SQL implementation
I've implemented the U-Net function just as a series of lateral cross-joins, without any recursive CTE or other tricks. This makes the nature of neural networks more obvious.
As usual, I'm using vanilla Postgres 17, without any extensions, and I'm not writing any procedural code either. To avoid excessive copy-pasting, I'm wrapping the basic blocks (like linear mappings, convolutions, sigmoid activations, and attention blocks) into pure SQL functions, which also don't have any procedural code.
Here's how it looks. Click on the title to expand the source; refresh the page to collapse it again. (I know it sucks; sorry about that.)
CREATE OR REPLACE FUNCTION EMB(_step INT)
RETURNS REAL[]
AS
$$
SELECT ARRAY_AGG(COS(value)) || ARRAY_AGG(SIN(value)) AS t_emb
FROM GENERATE_SERIES(0, 31) AS dim
CROSS JOIN LATERAL
(
SELECT _step * EXP(-LN(10000) * dim / 32.0) AS value
) q;
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION CONV2D3X3(_input REAL[][][], _weight REAL[][][][], _bias REAL[], _stride INT = 1)
RETURNS REAL[]
AS
$$
SELECT ARRAY_AGG(value)
FROM (
SELECT ARRAY_LENGTH(_input, 3) AS image_width,
ARRAY_LENGTH(_input, 2) AS image_height
) q1
CROSS JOIN LATERAL
GENERATE_SERIES(0, ARRAY_LENGTH(_weight, 1) - 1) AS c_out
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(value) AS value
FROM GENERATE_SERIES(0, image_height - 3 + 2, _stride) ky
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(value) AS value
FROM GENERATE_SERIES(0, image_width - 3 + 2, _stride) kx
CROSS JOIN LATERAL
(
SELECT SUM(
COALESCE(_input[c_in + 1][ky - 1 + 1][kx - 1 + 1], 0) * _weight[c_out + 1][c_in + 1][1][1] +
COALESCE(_input[c_in + 1][ky - 1 + 1][kx + 1], 0) * _weight[c_out + 1][c_in + 1][1][2] +
COALESCE(_input[c_in + 1][ky - 1 + 1][kx + 1 + 1], 0) * _weight[c_out + 1][c_in + 1][1][3] +
COALESCE(_input[c_in + 1][ky + 1][kx - 1 + 1], 0) * _weight[c_out + 1][c_in + 1][2][1] +
COALESCE(_input[c_in + 1][ky + 1][kx + 1], 0) * _weight[c_out + 1][c_in + 1][2][2] +
COALESCE(_input[c_in + 1][ky + 1][kx + 1 + 1], 0) * _weight[c_out + 1][c_in + 1][2][3] +
COALESCE(_input[c_in + 1][ky + 1 + 1][kx - 1 + 1], 0) * _weight[c_out + 1][c_in + 1][3][1] +
COALESCE(_input[c_in + 1][ky + 1 + 1][kx + 1], 0) * _weight[c_out + 1][c_in + 1][3][2] +
COALESCE(_input[c_in + 1][ky + 1 + 1][kx + 1 + 1], 0) * _weight[c_out + 1][c_in + 1][3][3] +
0
)
+ _bias[c_out + 1]
AS value
FROM GENERATE_SERIES(0, ARRAY_LENGTH(_weight, 2) - 1) AS c_in
) q
) q
) q2
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION CONV2D1X1(_input REAL[][][], _weight REAL[][][][], _bias REAL[], _stride INT = 1)
RETURNS REAL[]
AS
$$
SELECT ARRAY_AGG(value)
FROM (
SELECT ARRAY_LENGTH(_input, 3) AS image_width,
ARRAY_LENGTH(_input, 2) AS image_height
) q1
CROSS JOIN LATERAL
GENERATE_SERIES(0, ARRAY_LENGTH(_weight, 1) - 1) AS c_out
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(value) AS value
FROM GENERATE_SERIES(0, image_height - 1, _stride) ky
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(value) AS value
FROM GENERATE_SERIES(0, image_width - 1, _stride) kx
CROSS JOIN LATERAL
(
SELECT SUM(
COALESCE(_input[c_in + 1][ky + 1][kx + 1], 0) * _weight[c_out + 1][c_in + 1][1][1]
)
+ _bias[c_out + 1]
AS value
FROM GENERATE_SERIES(0, ARRAY_LENGTH(_weight, 2) - 1) AS c_in
) q
) q
) q2
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION LINEAR_1_2(_input REAL[], _weight REAL[][], _bias REAL[])
RETURNS REAL[]
AS
$$
SELECT ARRAY_AGG(value)
FROM GENERATE_SUBSCRIPTS(_weight, 1) l1
CROSS JOIN LATERAL
(
SELECT SUM(_input[l2] * _weight[l1][l2]) + _bias[l1] AS value
FROM GENERATE_SUBSCRIPTS(_weight, 2) l2
) q
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION LINEAR_2_2(_input REAL[][], _weight REAL[][], _bias REAL[])
RETURNS REAL[][]
AS
$$
SELECT ARRAY_AGG(value)
FROM GENERATE_SUBSCRIPTS(_input, 1) i1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(value) AS value
FROM GENERATE_SUBSCRIPTS(_weight, 1) w1
CROSS JOIN LATERAL
(
SELECT SUM(_input[i1][l2] * _weight[w1][l2]) + _bias[w1] AS value
FROM GENERATE_SUBSCRIPTS(_weight, 2) l2
)
) q
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION PLUS_3_1(_a REAL[][][], _b REAL[])
RETURNS REAL[]
AS
$$
SELECT ARRAY_AGG(v2)
FROM GENERATE_SUBSCRIPTS(_a, 1) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v3) AS v2
FROM GENERATE_SUBSCRIPTS(_a, 2) l2
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(_a[l1][l2][l3] + _b[l1]) AS v3
FROM GENERATE_SUBSCRIPTS(_a, 2) l3
)
) q
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION PLUS_3_2(_a REAL[][][], _b REAL[][])
RETURNS REAL[]
AS
$$
SELECT ARRAY_AGG(v2)
FROM GENERATE_SUBSCRIPTS(_a, 1) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v3) AS v2
FROM GENERATE_SUBSCRIPTS(_a, 2) l2
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(_a[l1][l2][l3] + _b[l1][l2]) AS v3
FROM GENERATE_SUBSCRIPTS(_a, 2) l3
)
) q
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION PLUS_3_3(_a REAL[][][], _b REAL[][])
RETURNS REAL[]
AS
$$
SELECT ARRAY_AGG(v2)
FROM GENERATE_SUBSCRIPTS(_a, 1) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v3) AS v2
FROM GENERATE_SUBSCRIPTS(_a, 2) l2
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(_a[l1][l2][l3] + _b[l1][l2][l3]) AS v3
FROM GENERATE_SUBSCRIPTS(_a, 2) l3
)
) q
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION SILU(_v REAL[])
RETURNS REAL[]
AS
$$
SELECT ARRAY_AGG(v * EXP(v) / (1 + EXP(v)))
FROM UNNEST(_v) AS v
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION SILU2(_v REAL[][])
RETURNS REAL[][]
AS
$$
SELECT ARRAY_AGG(v2)
FROM GENERATE_SUBSCRIPTS(_v, 1) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v * EXP(v) / (1 + EXP(v))) v2
FROM GENERATE_SUBSCRIPTS(_v, 1) l2
CROSS JOIN LATERAL
(
SELECT _v[l1][l2] AS v
) q
) q
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION SILU3(_v REAL[][][])
RETURNS REAL[][][]
AS
$$
SELECT ARRAY_AGG(v2)
FROM GENERATE_SUBSCRIPTS(_v, 1) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v3) AS v2
FROM GENERATE_SUBSCRIPTS(_v, 2) l2
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v * EXP(v) / (1 + EXP(v))) v3
FROM GENERATE_SUBSCRIPTS(_v, 3) l3
CROSS JOIN LATERAL
(
SELECT _v[l1][l2][l3] AS v
) q
) q
) q
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION GROUP_NORM(_image REAL[][][], _weight REAL[], _bias REAL[], _groups INT)
RETURNS REAL[][]
AS
$$
SELECT value
FROM (
SELECT ARRAY_LENGTH(_image, 1) / _groups AS group_size
) c
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(var_denominator) AS var_denominator,
ARRAY_AGG(mean) AS mean
FROM GENERATE_SERIES(0, ARRAY_LENGTH(_image, 1) -1, group_size) AS group_number
CROSS JOIN LATERAL
(
SELECT SQRT(VAR_SAMP(value) + 1e-05) AS var_denominator,
AVG(value) AS mean
FROM GENERATE_SERIES(0, group_size - 1) AS group_position
CROSS JOIN LATERAL
GENERATE_SUBSCRIPTS(_image, 2) iy
CROSS JOIN LATERAL
GENERATE_SUBSCRIPTS(_image, 3) ix
CROSS JOIN LATERAL
(
SELECT _image[group_number + group_position + 1][iy][ix] AS value
)
) q
) q1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(l1) AS value
FROM GENERATE_SERIES(0, ARRAY_LENGTH(_image, 1) - 1) AS channel
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(l2) AS l1
FROM GENERATE_SUBSCRIPTS(_image, 2) iy
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(l3) AS l2
FROM GENERATE_SUBSCRIPTS(_image, 3) ix
CROSS JOIN LATERAL
(
SELECT (_image[channel + 1][iy][ix] - mean[channel / group_size + 1]) / var_denominator[channel / group_size + 1] *
_weight[channel + 1] + _bias[channel + 1] AS l3
)
) q
) q
) q2
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION RESNET
(
_input REAL[],
_t_emb3 REAL[],
_norm1_weight REAL[],
_norm1_bias REAL[],
_conv1_weight REAL[],
_conv1_bias REAL[],
_time_emb_proj_weight REAL[],
_time_emb_proj_bias REAL[],
_norm2_weight REAL[],
_norm2_bias REAL[],
_conv2_weight REAL[],
_conv2_bias REAL[],
_conv_shortcut_weight REAL[],
_conv_shortcut_bias REAL[]
)
RETURNS REAL[]
AS
$$
SELECT hs9
FROM (
SELECT
) d
CROSS JOIN LATERAL
GROUP_NORM(_input, _norm1_weight, _norm1_bias, 32) hs2
CROSS JOIN LATERAL
SILU3(hs2) hs3
CROSS JOIN LATERAL
CONV2D3X3(hs3, _conv1_weight, _conv1_bias) hs4
CROSS JOIN LATERAL
LINEAR_1_2(_t_emb3, _time_emb_proj_weight, _time_emb_proj_bias) t_emb4
CROSS JOIN LATERAL
PLUS_3_1(hs4, t_emb4) hs5
CROSS JOIN LATERAL
GROUP_NORM(hs5, _norm2_weight, _norm2_bias, 32) hs6
CROSS JOIN LATERAL
SILU3(hs6) AS hs7
CROSS JOIN LATERAL
CONV2D3X3(hs7, _conv2_weight, _conv2_bias) hs8
CROSS JOIN LATERAL
(SELECT COALESCE(CONV2D1X1(_input, _conv_shortcut_weight, _conv_shortcut_bias), _input) input2) input2
CROSS JOIN LATERAL
PLUS_3_3(input2, hs8) hs9
$$
LANGUAGE SQL
IMMUTABLE
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION RESNET
(
_input REAL[],
_t_emb3 REAL[],
_prefix TEXT
)
RETURNS REAL[]
AS
$$
SELECT RESNET(
_input,
_t_emb3,
norm1.weight,
norm1.bias,
conv1.weight,
conv1.bias,
time_emb_proj.weight,
time_emb_proj.bias,
norm2.weight,
norm2.bias,
conv2.weight,
conv2.bias,
conv_shortcut.weight,
conv_shortcut.bias
) rn2
FROM (
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.norm1'
) norm1 (weight, bias)
CROSS JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.conv1'
) conv1 (weight, bias)
CROSS JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.time_emb_proj'
) time_emb_proj (weight, bias)
CROSS JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.norm2'
) norm2 (weight, bias)
CROSS JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.conv2'
) conv2 (weight, bias)
LEFT JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.conv_shortcut'
) conv_shortcut (weight, bias)
ON TRUE
$$
LANGUAGE SQL
STRICT
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION SCALED_DOT_PRODUCTION_ATTENTION
(
_query REAL[],
_key REAL[],
_value REAL[],
_head_dim INT
)
RETURNS REAL[]
AS
$$
SELECT scaled_reshaped
FROM (
SELECT ARRAY_LENGTH(_query, 2) / _head_dim AS heads,
1 / SQRT(_head_dim) AS scale_factor
) c
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v2) AS attn_weight
FROM GENERATE_SERIES(0, heads - 1) head
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v3) AS v2
FROM GENERATE_SUBSCRIPTS(_query, 1) qy
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(vexp) AS vexps
FROM GENERATE_SUBSCRIPTS(_key, 1) ky
CROSS JOIN LATERAL
(
SELECT EXP(SUM(_query[qy][head * _head_dim + x + 1] * _key[ky][head * _head_dim + x + 1]) * scale_factor) AS vexp
FROM GENERATE_SERIES(0, _head_dim - 1) x
) l4
) l3
CROSS JOIN LATERAL
(
SELECT SUM(vexp) AS denominator
FROM UNNEST(vexps) vexp
) q
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(vexp / denominator) AS v3
FROM UNNEST(vexps) vexp
) q2
) l2
) hs1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v2) AS scaled_reshaped
FROM GENERATE_SUBSCRIPTS(attn_weight, 2) y
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v3) AS v2
FROM GENERATE_SERIES(0, heads - 1) head
CROSS JOIN LATERAL
GENERATE_SERIES(0, _head_dim - 1 + head - head) hc
CROSS JOIN LATERAL
(
SELECT SUM(attn_weight[head + 1][y][ax] * _value[ax][head * _head_dim + hc + 1]) AS v3
FROM GENERATE_SUBSCRIPTS(attn_weight, 3) ax
) l3
) l2
) hs2
$$
LANGUAGE SQL
IMMUTABLE
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION ATTN
(
_input REAL[],
_group_norm_weight REAL[],
_group_norm_bias REAL[],
_to_q_weight REAL[],
_to_q_bias REAL[],
_to_k_weight REAL[],
_to_k_bias REAL[],
_to_v_weight REAL[],
_to_v_bias REAL[],
_to_out_weight REAL[],
_to_out_bias REAL[]
)
RETURNS REAL[]
AS
$$
SELECT attn
FROM (
SELECT ARRAY_LENGTH(_input, 1) AS channel,
ARRAY_LENGTH(_input, 2) AS height,
ARRAY_LENGTH(_input, 3) AS width
) c
CROSS JOIN LATERAL
GROUP_NORM(_input, _group_norm_weight, _group_norm_bias, 32) hs2
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v2) AS hs3
FROM GENERATE_SUBSCRIPTS(hs2, 2) l2
CROSS JOIN LATERAL
GENERATE_SUBSCRIPTS(hs2, 3 + (l2 - l2)) l3
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(hs2[l1][l2][l3]) v2
FROM GENERATE_SUBSCRIPTS(hs2, 1) l1
)
) hs3
CROSS JOIN LATERAL
LINEAR_2_2(hs3, _to_q_weight, _to_q_bias) query
CROSS JOIN LATERAL
LINEAR_2_2(hs3, _to_k_weight, _to_k_bias) key
CROSS JOIN LATERAL
LINEAR_2_2(hs3, _to_v_weight, _to_v_bias) value
CROSS JOIN LATERAL
SCALED_DOT_PRODUCTION_ATTENTION(query, key, value, 8) scaled_reshaped
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v2) AS hs4
FROM GENERATE_SUBSCRIPTS(_to_out_weight, 1) oy
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v3) AS v2
FROM GENERATE_SERIES(0, height - 1) ch
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v4) AS v3
FROM GENERATE_SERIES(0, width - 1) cw
CROSS JOIN LATERAL
(
SELECT ch * height + cw + 1 AS scy
) q
CROSS JOIN LATERAL
(
SELECT SUM(scaled_reshaped[scy][x] * _to_out_weight[oy][x]) + _to_out_bias[oy] AS v4
FROM GENERATE_SUBSCRIPTS(scaled_reshaped, 2) x
) l4
) l3
) l2
) hs4
CROSS JOIN LATERAL
PLUS_3_3(hs4, _input) AS attn
$$
LANGUAGE SQL
IMMUTABLE
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION ATTN
(
_input REAL[],
_prefix TEXT
)
RETURNS REAL[]
AS
$$
SELECT ATTN(
_input,
group_norm.weight,
group_norm.bias,
to_q.weight,
to_q.bias,
to_k.weight,
to_k.bias,
to_v.weight,
to_v.bias,
to_out.weight,
to_out.bias
) rn2
FROM (
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.group_norm'
) group_norm (weight, bias)
CROSS JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.to_q'
) to_q (weight, bias)
CROSS JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.to_k'
) to_k (weight, bias)
CROSS JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.to_v'
) to_v (weight, bias)
CROSS JOIN
(
SELECT weight::TEXT::REAL[], bias::TEXT::REAL[]
FROM parameters
WHERE key = _prefix || '.to_out.0'
) to_out (weight, bias)
$$
LANGUAGE SQL
STRICT
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION UPSAMPLE_NEAREST2D_3_SCALE_2(_image REAL[][][])
RETURNS REAL[][][]
AS
$$
SELECT ARRAY_AGG(v1)
FROM GENERATE_SUBSCRIPTS(_image, 1) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v2) AS v1
FROM GENERATE_SUBSCRIPTS(_image, 2) l2
CROSS JOIN LATERAL
GENERATE_SERIES(0, 1 + l2 - l2)
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(_image[l1][l2][l3]) AS v2
FROM GENERATE_SUBSCRIPTS(_image, 3) l3
CROSS JOIN LATERAL
GENERATE_SERIES(0, 1 + l3 - l3)
) l3
) l2
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
Here's the implementation of the whole U-Net function:
CREATE OR REPLACE FUNCTION UNET(_image REAL[][][], _step INT)
RETURNS REAL[][][]
AS
$$
SELECT out
FROM EMB(_step) t_emb
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'time_embedding.linear_1') t_embp1 (weight, bias)
CROSS JOIN LATERAL LINEAR_1_2(t_emb, t_embp1.weight, t_embp1.bias) t_emb2
CROSS JOIN SILU(t_emb2) t_emb3
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'time_embedding.linear_2') t_embp2 (weight, bias)
CROSS JOIN LATERAL LINEAR_1_2(t_emb3, t_embp2.weight, t_embp2.bias) t_emb4
CROSS JOIN SILU(t_emb4) t_emb5
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'conv_in') conv_in (weight, bias)
CROSS JOIN LATERAL CONV2D3X3(_image, conv_in.weight, conv_in.bias) input1
-- Down 1
CROSS JOIN LATERAL RESNET(input1, t_emb5, 'down_blocks.0.resnets.0') db0rn0
CROSS JOIN LATERAL RESNET(db0rn0, t_emb5, 'down_blocks.0.resnets.1') db0rn1
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'down_blocks.0.downsamplers.0.conv') db0ds (weight, bias)
CROSS JOIN LATERAL CONV2D3X3(db0rn1, db0ds.weight, db0ds.bias, 2) AS db0
-- Down 2
CROSS JOIN LATERAL RESNET(db0, t_emb5, 'down_blocks.1.resnets.0') db1rn0
CROSS JOIN LATERAL RESNET(db1rn0, t_emb5, 'down_blocks.1.resnets.1') db1rn1
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'down_blocks.1.downsamplers.0.conv') db1ds (weight, bias)
CROSS JOIN LATERAL CONV2D3X3(db1rn1, db1ds.weight, db1ds.bias, 2) AS db1
-- Down 3 with Attention
CROSS JOIN LATERAL RESNET(db1, t_emb5, 'down_blocks.2.resnets.0') db2rn0
CROSS JOIN LATERAL ATTN(db2rn0, 'down_blocks.2.attentions.0') db2att0
CROSS JOIN LATERAL RESNET(db2att0, t_emb5, 'down_blocks.2.resnets.1') db2rn1
CROSS JOIN LATERAL ATTN(db2rn1, 'down_blocks.2.attentions.1') db2att1
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'down_blocks.2.downsamplers.0.conv') db2ds (weight, bias)
CROSS JOIN LATERAL CONV2D3X3(db2att1, db2ds.weight, db2ds.bias, 2) AS db2
-- Down 4 with Attention
CROSS JOIN LATERAL RESNET(db2, t_emb5, 'down_blocks.3.resnets.0') db3rn0
CROSS JOIN LATERAL ATTN(db3rn0, 'down_blocks.3.attentions.0') db3att0
CROSS JOIN LATERAL RESNET(db3att0, t_emb5, 'down_blocks.3.resnets.1') db3rn1
CROSS JOIN LATERAL ATTN(db3rn1, 'down_blocks.3.attentions.1') db3
-- Mid
CROSS JOIN LATERAL RESNET(db3, t_emb5, 'mid_block.resnets.0') mbrn0
CROSS JOIN LATERAL ATTN(mbrn0, 'mid_block.attentions.0') mbatt0
CROSS JOIN LATERAL RESNET(mbatt0, t_emb5, 'mid_block.resnets.1') mb
-- Up 1 with Attention
CROSS JOIN LATERAL RESNET(mb || db3, t_emb5, 'up_blocks.0.resnets.0') ub0rn0
CROSS JOIN LATERAL ATTN(ub0rn0, 'up_blocks.0.attentions.0') ub0att0
CROSS JOIN LATERAL RESNET(ub0att0 || db3att0, t_emb5, 'up_blocks.0.resnets.1') ub0rn1
CROSS JOIN LATERAL ATTN(ub0rn1, 'up_blocks.0.attentions.1') ub0att1
CROSS JOIN LATERAL RESNET(ub0att1 || db2, t_emb5, 'up_blocks.0.resnets.2') ub0rn2
CROSS JOIN LATERAL ATTN(ub0rn2, 'up_blocks.0.attentions.2') ub0att2
CROSS JOIN UPSAMPLE_NEAREST2D_3_SCALE_2(ub0att2) ub0us1
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'up_blocks.0.upsamplers.0.conv') ub0us (weight, bias)
CROSS JOIN CONV2D3X3(ub0us1, ub0us.weight, ub0us.bias) ub0
-- Up 2 with Attention
CROSS JOIN LATERAL RESNET(ub0 || db2att1, t_emb5, 'up_blocks.1.resnets.0') ub1rn0
CROSS JOIN LATERAL ATTN(ub1rn0, 'up_blocks.1.attentions.0') ub1att0
CROSS JOIN LATERAL RESNET(ub1att0 || db2att0, t_emb5, 'up_blocks.1.resnets.1') ub1rn1
CROSS JOIN LATERAL ATTN(ub1rn1, 'up_blocks.1.attentions.1') ub1att1
CROSS JOIN LATERAL RESNET(ub1att1 || db1, t_emb5, 'up_blocks.1.resnets.2') ub1rn2
CROSS JOIN LATERAL ATTN(ub1rn2, 'up_blocks.1.attentions.2') ub1att2
CROSS JOIN UPSAMPLE_NEAREST2D_3_SCALE_2(ub1att2) ub1us1
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'up_blocks.1.upsamplers.0.conv') ub1us (weight, bias)
CROSS JOIN CONV2D3X3(ub1us1, ub1us.weight, ub1us.bias) ub1
-- Up 3
CROSS JOIN LATERAL RESNET(ub1 || db1rn1, t_emb5, 'up_blocks.2.resnets.0') ub2rn0
CROSS JOIN LATERAL RESNET(ub2rn0 || db1rn0, t_emb5, 'up_blocks.2.resnets.1') ub2rn1
CROSS JOIN LATERAL RESNET(ub2rn1 || db0, t_emb5, 'up_blocks.2.resnets.2') ub2rn2
CROSS JOIN UPSAMPLE_NEAREST2D_3_SCALE_2(ub2rn2) ub2us1
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'up_blocks.2.upsamplers.0.conv') ub2us (weight, bias)
CROSS JOIN CONV2D3X3(ub2us1, ub2us.weight, ub2us.bias) ub2
-- Up 4
CROSS JOIN LATERAL RESNET(ub2 || db0rn1, t_emb5, 'up_blocks.3.resnets.0') ub3rn0
CROSS JOIN LATERAL RESNET(ub3rn0 || db0rn0, t_emb5, 'up_blocks.3.resnets.1') ub3rn1
CROSS JOIN LATERAL RESNET(ub3rn1 || input1, t_emb5, 'up_blocks.3.resnets.2') ub3
-- Decode
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'conv_norm_out') conv_norm_out (weight, bias)
CROSS JOIN LATERAL GROUP_NORM(ub3, conv_norm_out.weight, conv_norm_out.bias, 32) conv_norm_out1
CROSS JOIN LATERAL SILU3(conv_norm_out1) conv_norm_out2
CROSS JOIN (SELECT weight::TEXT::REAL[], bias::TEXT::REAL[] FROM parameters WHERE key = 'conv_out') conv_out (weight, bias)
CROSS JOIN LATERAL CONV2D3X3(conv_norm_out2, conv_out.weight, conv_out.bias) out
$$
LANGUAGE SQL
STRICT
LEAKPROOF
PARALLEL SAFE;
The model parameters are stored in PostgreSQL arrays in a table. At the bottom of this post, you will find a link to the GitHub repository with the source code of all the functions and a script to download the model from HuggingFace and upload it to the database.
Let's try running a single pass of the U-Net on a random input and see where it gets us. This query generates a 3×64×64 array of random pixels and pipes it through U-Net. The result is also an array of the same shape. It's supposed to represent an estimation of noise: a vector, which, when subtracted from the input, would yield having some features of a butterfly.
For brevity, I'm only returning the first two items from each of the resulting array's dimensions, and also its general shape.
Here's the query:
SELECT SETSEED(0.20241231);
WITH initial_image (input) AS MATERIALIZED
(
SELECT ARRAY_AGG(v)
FROM GENERATE_SERIES(1, 3) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v) v
FROM GENERATE_SERIES(1, 64) l2
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(RANDOM()::REAL) v
FROM GENERATE_SERIES(1, 64) l3
) l3
) l3
)
SELECT unet[1:2][1:2][1:2], ARRAY_DIMS(unet)
FROM UNET((SELECT input FROM initial_image), 999) unet
| unet | array_dims |
|---|---|
| [[[0.37433589, 0.56223816], [-0.14284264, 0.112475105]], [[-0.070850156, 0.45626032], [0.08289513, 0.79304886]]] | [1:3][1:64][1:64] |
It works and takes a whopping 24 minutes on my machine. Just a single pass through U-Net.
Doing this 1000 times in a row would take 24000 minutes, or a little under 17 days. And New Year's Eve is only hours away.
Shit.
Can we fix it somehow?
Skipping the steps
Earlier, we told our model not to make hasty assumptions about its predictions and instead do the reconstruction of the images in smaller steps. Instead of cancelling predicted noise all at once, that is, going from "sample" to "sample minus the noise" for every pixel, we would treat it as a general direction. Mathematically, it would mean that we should add a certain percentage of the original pixel value with a certain percentage of the denoised pixel. We do just enough of that so as to end up at the level of noise that would have been added on the previous step. Then we would run the model again and make a more correct prediction.
What if we want to skip some steps? Instead of cancelling just a little bit of noise and ending up at the previous step, we would cancel more of it and end up several steps earlier. Of course, that would throw all the math off, and we would not arrive at the same distribution of images that going through every step separately would end us. However, for the purposes of making ASCII SQL art in a terminal, it could be just enough.
The model that we are using is trained to evaluate the noise vector. It could have been made to evaluate the original image or the mean of the distribution of the previous image, conditioned on the subsequent one. Mathematically, it's all the same, and closed-form expressions exist to convert between all three of these values.
However, the trained model that we are using is not exactly following the path outlined in the paper. Its backbone function returns the estimation of noise, and from this estimation, on each step, the image from the previous step is sampled. The closed-form expression for this operation, per the paper, is this:
But the model doesn't use this expression. It first calculates the estimation of the original image, then clamps it to the range of , and then samples a point from the distribution on the target step, conditioned on the clamped estimation of the original image:
Now, let me digress a little while it's still fresh in my memory. Remember the pseudocode that demonstrated the use of the noise scheduler? There was a mysterious line saying "add noise." The last term in the expression, , is doing just that.
is sampled from the standard Gaussian distribution and
is calculated from the noise schedule. Now, why would we want to add back noise that we were working so hard to remove?
The expression in the brackets has the same mean as the distribution of images that would be generated by the Markov chain, but lower variance. In practice it means that had we used this expression, the model would be less creative than it could be. The set of results it would be likely to generate would be narrower and closer to the model's "idea" of an idealized, generic butterfly.
Here's what we get if we don't add this noise:

Those all are butterflies alright, and they're all even technically different. But, I mean, come on. According to the model, this is what an "average" butterfly looks like, and if we sample from the distribution that doesn't vary a lot, all we get are samples from the closest vicinity of that "average."
By increasing the variance and sampling from the theoretic distribution, we make sure that the model can generate a wider range of images that we humans would still recognize as a butterfly.
Ok, back to skipping the steps. The expression above can be generalized to produce the estimation of the image on an arbitrary step:
The expression for the sigma doesn't match the theoretical value, but it's good enough for our purposes.
Experiments show that making just four steps on the following schedule: , is enough to generate realistic enough images of butterflies:

To implement the scheduler, we'll need to create several more SQL functions:
CREATE OR REPLACE FUNCTION PREDICT_PREVIOUS(_image REAL[][][], _noise REAL[][][], _t INT, _t2 INT)
RETURNS REAL[][][]
AS
$$
WITH alphas_p AS
(
SELECT EXP(SUM(LN(1 - ((0.02 - 0.0001) * step / 999 + 0.0001))) OVER (ORDER BY step)) AS alphas_p,
step
FROM GENERATE_SERIES(0, 999) step
)
SELECT v1
FROM (
SELECT alphas_p AS alphas_p_t
FROM alphas_p
WHERE step = _t
) q_t
CROSS JOIN LATERAL
(
SELECT alphas_p AS alphas_p_t2
FROM alphas_p
WHERE step = _t2
) q_t2
CROSS JOIN LATERAL
(
SELECT SQRT(alphas_p_t2) * (1 - alphas_p_t / alphas_p_t2) / (1 - alphas_p_t) AS x0_c,
SQRT(alphas_p_t / alphas_p_t2) * (1 - alphas_p_t2) / (1 - alphas_p_t) AS xt2_c
)
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v2) AS v1
FROM GENERATE_SUBSCRIPTS(_image, 1) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v3) AS v2
FROM GENERATE_SUBSCRIPTS(_image, 2) l2
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(image_t2) AS v3
FROM GENERATE_SUBSCRIPTS(_image, 3) l3
CROSS JOIN LATERAL
(
SELECT _image[l1][l2][l3] AS image,
_noise[l1][l2][l3] AS noise
) q
CROSS JOIN LATERAL
(
SELECT GREATEST(LEAST((image - noise * SQRT(1 - alphas_p_t)) / SQRT(alphas_p_t), 1), -1) AS x0
) x0
CROSS JOIN LATERAL
(
SELECT x0_c * x0 + xt2_c * image AS image_t2
) image_t2
) l3
) l2
) l1
$$
LANGUAGE SQL
IMMUTABLE
STRICT
LEAKPROOF
PARALLEL SAFE;
CREATE OR REPLACE FUNCTION GENERATE_NOISE()
RETURNS REAL[][][]
AS
$$
WITH initial_image (input) AS MATERIALIZED
(
SELECT ARRAY_AGG(v)
FROM GENERATE_SERIES(1, 3) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v) v
FROM GENERATE_SERIES(1, 64) l2
CROSS JOIN LATERAL
(
-- Introduce dependency, otherwise GENERATE_SERIES(1, 64) will be cached and generate duplicates
-- The distribution is uniform, but has the same mean and variance as the standard normal distribution
SELECT ARRAY_AGG((RANDOM()::REAL * 2 - 1) * 1.73 + l1 + l2 + l3 - l1 - l2 - l3) v
FROM GENERATE_SERIES(1, 64) l3
) l3
) l3
)
SELECT input
FROM initial_image
$$
LANGUAGE SQL;
CREATE OR REPLACE FUNCTION GENERATE_CREATIVE_NOISE(_t INT, _t2 INT)
RETURNS REAL[][][]
AS
$$
WITH alphas_p AS
(
SELECT EXP(SUM(LN(1 - ((0.02 - 0.0001) * step / 999 + 0.0001))) OVER (ORDER BY step)) AS alphas_p,
step
FROM GENERATE_SERIES(0, 999) step
)
SELECT ARRAY_AGG(v)
FROM (
SELECT alphas_p AS alphas_p_t
FROM alphas_p
WHERE step = _t
) q_t
CROSS JOIN LATERAL
(
SELECT alphas_p AS alphas_p_t2
FROM alphas_p
WHERE step = _t2
) q_t2
CROSS JOIN LATERAL
(
SELECT SQRT((1 - alphas_p_t2) / (1 - alphas_p_t) * (1 - alphas_p_t / alphas_p_t2)) AS creative_noise_c
) q1
CROSS JOIN LATERAL
GENERATE_SERIES(1, 3) l1
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG(v) v
FROM GENERATE_SERIES(1, 64) l2
CROSS JOIN LATERAL
(
SELECT ARRAY_AGG((RANDOM()::REAL * 2 - 1) * 1.73 * creative_noise_c + l1 + l2 + l3 - l1 - l2 - l3) v
FROM GENERATE_SERIES(1, 64) l3
) l3
) l3
$$
LANGUAGE SQL;
The image
Let's run the scheduler!
The query below completes in 101 minutes and generates an image of a butterfly:
WITH initial_image (input) AS MATERIALIZED
(
SELECT GENERATE_NOISE()
)
SELECT v2
FROM (SELECT)
CROSS JOIN LATERAL UNET((SELECT input FROM initial_image), 500) unet1
CROSS JOIN LATERAL PREDICT_PREVIOUS((SELECT input FROM initial_image), unet1, 500, 250) step1
CROSS JOIN LATERAL GENERATE_CREATIVE_NOISE(500, 250) noise1
CROSS JOIN PLUS_3_3(step1, noise1) image2
CROSS JOIN LATERAL UNET(image2, 250) unet2
CROSS JOIN LATERAL PREDICT_PREVIOUS(image2, unet2, 250, 125) step2
CROSS JOIN LATERAL GENERATE_CREATIVE_NOISE(250, 125) noise2
CROSS JOIN PLUS_3_3(step2, noise2) image3
CROSS JOIN LATERAL UNET(image3, 125) unet3
CROSS JOIN LATERAL PREDICT_PREVIOUS(image3, unet3, 125, 60) step3
CROSS JOIN LATERAL GENERATE_CREATIVE_NOISE(125, 60) noise3
CROSS JOIN PLUS_3_3(step3, noise3) image4
CROSS JOIN LATERAL UNET(image4, 60) unet4
CROSS JOIN LATERAL PREDICT_PREVIOUS(image4, unet4, 60, 0) butterfly
CROSS JOIN LATERAL
(
SELECT STRING_TO_ARRAY(' `.-'':_,^=;><+!rc*/z?sLTv)J7(|Fi{C}fI31tluneoZ5Yxjya]2ESwqkP6h9d4VpOGbUAKXHm8RD#Bg0MNWQ%&@', NULL) AS codes
)
CROSS JOIN LATERAL
(
SELECT v2
FROM GENERATE_SUBSCRIPTS(butterfly, 2) y
CROSS JOIN LATERAL
(
SELECT STRING_AGG(code, '') v2
FROM GENERATE_SUBSCRIPTS(butterfly, 3) x
CROSS JOIN LATERAL
(
SELECT FLOOR(LEAST(GREATEST(AVG(-v) * 2 - 1 + 1, 0), 1) * (ARRAY_LENGTH(codes, 1) - 1))::INT + 1 AS brightness
FROM UNNEST(butterfly[1:3][y:y][x:x]) v
)
CROSS JOIN LATERAL
(
SELECT codes[brightness] AS code
)
)
)
| v2 |
|---|
| , cJz |
| s]TrFCe- ,fZYo]- |
| eEJY?7TvyL r )Il5F(ai' |
| /n_fTvt{*t9{r }( .vJ1Sc+IJi7T |
| rJ?T/J3e:zj4Zu }lEkF,F7eFC- |
| z;)iv*tluyheyy )cTllnv iY3FIy |
| V3u1z fnzf*|{FP= |1L>^Ex{1xeu)}q |
| _S}z,=>ixr.*77TFr- | zj1wY` Lwue3Cuate |
| ya?'L}?ff(<FjTJJl]` _ * |FECq3-!)>T)J:/TSo |
| |ZYzcFivJan=?](c:<oIF .3r vf5Z|nC3|; ;ix?;J4, |
| zZIL- Tvnjufwnr_++? ;, * 'o|TofsL'^i: )!s(/^Z |
| ,wt|z `on=)FeIxEl{t ' i su))oy1{<'L^ cl5|Iv} |
| 21v|z}F5;->!sfhkn>iT! <s - cl_,cJ{s(t7nh5 ?'vT3I/L^ |
| yx)r)1PEF};+<unlt}Co<*f|. uI,>(vLJ}?JZuu+c:YJv))^_ |
| ]17r;nuJ|ou< ct!(]yeiiY> >vT(Tc/;J7vv +L++{*1_TvYT |
| o1:r7fCL|I3:`/rnfty23It<T+ ,s|C<|1?f/. !?n/|3f7/i) |
| !|}II]{c.rv iq]nT?Jvo=C{r s3uczf!/F;! `iC3ud]}3}i< |
| cz]2ftL < fPYz>JcJfiC}r c ?ijL)J<s/< >'Llfxy7L>-, |
| ax5{ >z1CJ>>ie{c :?+ s ,j3r)Is/c `TCICJI_< |
| rJu^ /IJ?/)nEZaL:ce, _ -o2s/F(Jz .lhJ{i/r |
| (r7Li; + *tL;z(oxn2]F)7C< - . J2!*n(/,c!_. ! !Jh]i T '. |
| ^Cviss* .;CEwt7C)3JCFeJ:?3e:'` Jn|F?T*I`, ^c >v/ l, |
| t?-r* v ,J*{Ls{*J>FT(s'z(*,j]7'*7fF|?f5z> 'z! v|r | |
| ;! 7 !_- `!+J zf{7{nv*FzF!Lxx)13>*ife1i(!=+rc=J+ vC =I |
| : ^;<^ ),nuT^<u7Lt3=^(35593te ltf{<L> TTz+(}r <:*; |
| s: :-^zC 'Lrf}q)i{>(nhlsFJt74e3C<>*=}i7z, >5c!,{=` *| |{ |
| } !r!tz/ *J ,v=<IoquZuf<1|(Suua+*c<C5|zo>F<=TC(|.JL /;r |
| /{}}](71' />`C(.*}L7YTl{/FEy1lP]ifFsfu1?iFFC}l3]tI^L L7 |
| )SE3oCcJ vlFiFJl})v< /)<V3}*osokxu]x<xy]P{xVxJzY1n1|{ ;ft |
| {y}c|({3:`ISxJC)x|fc J!J1Ls}ftL({vfF}Z1Ep6]eYF(?|L+zv}Yv_ |
| z< :Z;LC3YaY/` z{1?_zl/s)7f(?{}Fo7TliY2f)|Ifour<I/!!-I! |
| i= '+`?)}fiJiz:c?3}se| F7-_{jlIF` '!T}Y* veC}F)L};</ . |
| ? ; }ssscvcI!zsxYt{(!!L s1x)vFcfz>c/Ji/ c( ,f{f}r , + |
| ''r?!?C}T '3I-`;:za+^nvCtxjLv{CZkC{ r}f77T31FrCY> |
| :. s(xY|</,** '/, >l+Lc /1rTFros/sv3; '_:|iC,YyCiifYz_ |
| ; ia9Y /r =_ ^|F <z 7/! ^*/!sc3l;,T1FuC! v=z !l{Y` |
| +33nl}f3? )v^ , :v!.,. : =+3:TvL}CZC(^.c;c /zi5l7 |
| oPZEe31F '_ .7F_szs? + ,|J,/((3Yno1uz7!<{7jnnuif |
| r6U5YoCY* uC=zc/< :. c<t!_ *)fTFLFCSE{v`^{!=!Zy}Z2y |
| z3p6Ylli(`: 1 r7c*7) r+,' !L !ICi)/?'+CZ1t=`^< ;Cf3}o |
| Pmee{qp_ v ?T L`!c - *L(L7|ir-*- `+ZS- z7LYz |
| *PSj9t1?+) J/.:/<`! !- c+/ +Ct?su3L`- +Ii<` |(FhZ/ |
| _ sUBqGIiiJc-?c (cv}?,__`= 7c +v/!s ^ LIF52s^' |
| k9axoi,_ :s?uC(sr*- (f ^=+-, . L?`:+,CSqts |
| I9IIlJ;;>L' ^?>}aT7 rf .,}; =f)' '* T5i;_*_,)7i+ |
| ,13aoSw3c} =!7Fs>' oSZ, vl1J:`^. {;lJ ,;' <?<F |
| l6nIhEr. ?+' s]7J`_ +I)!``Fi`' ^'+sFzrs^*+;<YEc |
| _;TII51J *_` .!L T1+: = zJ ^xq( - ?i!_< ` Ce|<3z(> |
| C5ne)J+ C zL ; ' >z><t|+<-|yFvv*|i+ '^ +zCuIi_r |
| _xujqfz.zjY!!JI/ =*.> 7 *)A| /s?}s/Jc=`'? /7Clf>_ |
| +yaCFPqFr`?*Jr+t?t7+ T V1L rfz7? L}L(t> c TL/_ |
| -f}c/}e3x{:_;`JCsf((: - Tq/ ^)zC)?'J/*y}- -;CCea |
| /3C`r!us|/T?7)r)(l1/? CZz<'>CFluT{TzLi=^ >n37nl |
| -{l{r|isau},vs*JLi{< jxZl*Ji1FLLu?J * ^+J7io| |
| ')5iCfqwhs)+L/!?)<r` ` (jo:v1=+cT3( { znZ. |
| ;1^7twS1]o3:(o|(/ c . Tscn>:. ^ `TF1l |
| r7-ro7o19k?npZ{; lzr+/:<s = )/|i> |
| !: |u5}fv )7ut! =z^ *;+L`/--* ; /ZZ*?s |
| , +x5j?u;vF-: 7z _*k7s.zns+|tvZ]u/* |
| < L >l1+ ? .}L3Zcs(j7s|_Z)|, |
| iPl .f3 cJtnv^ )C < |
| = : s |

May the New Year bring you bright colors and make you spread your wings like a butterfly!
You can find the queries and the installation code in the GitHub repository: quassnoi/explain-extended-2025
Previous New Year posts:
- 2010: SQL graphics in Oracle, MySQL, SQL Server and PostgreSQL
- 2011: Drawing a clock in SQL
- 2012: Drawing snowflakes in SQL
- 2013: View of Earth from space in SQL
- 2014: Drawing fractals in SQL
- 2015: Composing music in SQL
- 2016: Conway’s Game of Life in SQL
- 2017: The Sultan’s Riddle in SQL
- 2018: Settlers of Catan in SQL
- 2019: GIF decoder in SQL
- 2020: A stereogram in SQL
- 2021: 3D picture of the coronavirus in SQL
- 2022: Quantum computer emulator in SQL
- 2023: Solving the Rubik’s Cube in SQL
- 2024: GPT in 500 lines of SQL

 Subscribe in a reader
Subscribe in a reader
Great article!!!
I’m trying to think of how to do this with SQL Server and my head is exploding.
Thank’s by all.
Manolo garcia
3 Jan 25 at 10:52
From here, there is a suggestion at the end that suggests a PostGIS -> PNG convertor? Possible/Feasible? Way beyond me, but would you be interested? Love your work by the way – we exchanged comments on dba.stackexchange. Best regards…
Pól Ua Laoínecháin
19 Jul 25 at 19:57
Forgot website: https://blog.jooq.org/fun-with-postgis-mandelbrot-set-game-of-life-and-more/. À+…
Pól Ua Laoínecháin
19 Jul 25 at 19:59
I’m not sure what PostGIS to PNG converter would do (the former is an extension that adds spatial functions and indexes to PostgreSQL; the latter is an image format). I have implemented a GIF decoder in SQL if it counts: https://explainextended.com/2018/12/31/happy-new-year-10/
And of course I implemented both the Mandelbrot set: https://explainextended.com/2013/12/31/happy-new-year-5/ and the Game of Life: https://explainextended.com/2015/12/31/happy-new-year-7/ a long long time ago.
Quassnoi
20 Jul 25 at 05:40