Things SQL needs: determining range cardinality
What is the problem with this query?
SELECT *
FROM orders
WHERE quantity <= 4
AND urgency <= 4
The problem is indexing strategy, of course. Which columns should we index?
If we index quantity, the optimizer will be able to use the index to filter on it. However, filtering on urgency will require scanning all records with quantity < 4 and applying the urgency filter to each record found.
Same with urgency. We can use range access on urgency using an index, but this will require filtering on quantity.
Why, create a composite index!
, some will say.
Unfortunately, that won't help much.
A composite B-Tree index maintains what is called a lexicographical order of the records. This means that an index on (quantity, urgency) will sort on quantity, and only if the quantities are equal, it will take the urgency into account.
The picture below shows how would the records be ordered in such an index:
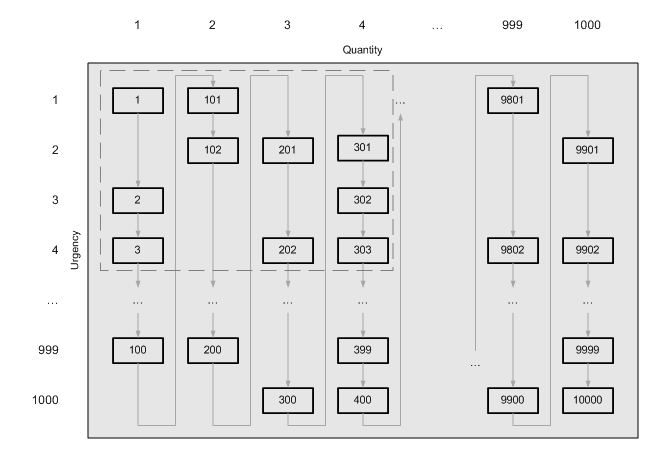
As we can see, with a single index range scan (i. e. just following the arrows) we cannot select only the records within the dashed rectangle. There is no single index range that could be used to filter on both columns.
Even if we changed the field order in the index, it would just change the direction of the arrows connecting the records:
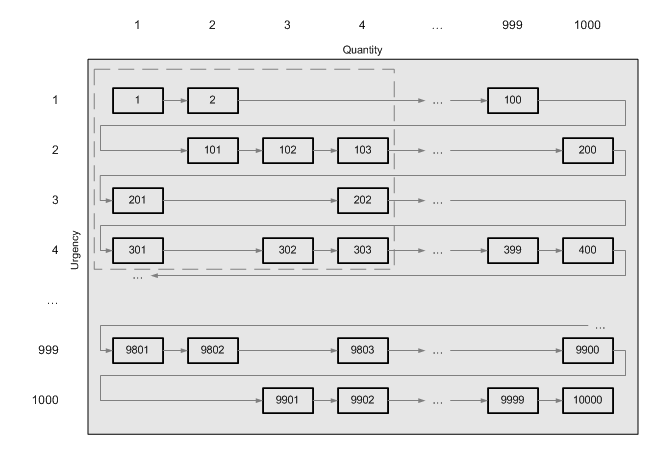
, and still no single range that contains only the records we need.
Can we improve it?
If we take at closer look at the table contents we will see that despite the fact that there is no single range that contains the records we need (and only them), there are four ranges that do filter our records.
If we rewrote the query condition like that:
SELECT * FROM orders WHERE quantity IN (0, 1, 2, 3, 4) AND urgency <= 4
with the first index, or like that:
SELECT *
FROM orders
WHERE quantity <= 4
AND urgency IN (0, 1, 2, 3, 4)
with the second index, then any decent SQL engine would build a decent and efficient plan (Index range in MySQL, INLIST ITERATOR in Oracle etc.)
The problem is that rewriting this query still requires an SQL developer. But this could be done automatically by the optimizer. There are several methods to do that.
Smallest superset
A range condition defines a set of the values that could possibly satisfy the condition (i. e. belong to the range). The number
of the values that satisfy this condition is called set cardinality. The word number is quoted here because it can be infinite, and not all infinities are created equal: some are more infinite than the others!
However, if we take the column definition into account, we can see that some ranges define finite (and quite constrained) sets of possible values. For instance, a condition like quantity < 4 on a column that is defined as UNSIGNED INT can possibly be satisfied by five values: 0, 1, 2, 3 and 4.
This set is the smallest superset of all sets of values that satisfy the range condition.
Loose index scan
Even with the conditions that theoretically define the infinite sets of values that could satisfy them, practically there is always a finite number of values in the table that do satisfy them (the table itself contains the finite number of records, to begin with).
And most engines keep track of that number in their statistics tables: this is what is called field cardinality, a measure of field uniqueness.
If the range cardinality is expected to be low (either from the set of values that can possibly belong to the range, or from the actual number of distinct values that do belong to the range, according to statistics), it would be a wise idea to rewrite the range condition as an IN condition containing all possible values that can belong or do belong to the range.
This will replace a single less than
or greater then
with a small number of equals to
. And an equals to
gives the optimizer much more space to, um, optimize. It can use a HASH JOIN, split the index into a number of continuous ranges or do some other interesting things that can only be done with an equijoin.
With an UNSIGNED INTEGER column, it is easy to generate a set of values that could satisfy the range. But what if we know the range cardinality to be low from the statistics, not from the column datatype?
In this case, we could build the set of possible values using what MySQL calls a loose index scan.
Basically, it takes the first record from the index and then recursively searches the next lowest record whose key value is greater than the previous one, using the index seek (as opposed to index scan). This means instead of mere scanning the index and applying the condition to each field, the engine would walk up and down the B-Tree to locate the first record the the greater key. It is much more efficient when the number of distinct keys is small. And in fact, MySQL does use this method for queries that involve SELECT DISTINCT on an indexed field.
MIN / MAX
This method would be useful for the open ranges (like > or <, as opposed to BETWEEN).
By default, the INT column means SIGNED INT. For a condition like quantity <= 4 this would mean all integers from -2,147,483,647 to 4 which is way too many.
In real tables, the quantities would be something greater than 0. But not all developers bother to pick a right datatype or add CHECK constraints for their columns (and some databases like PostgreSQL lack the unsigned datatypes anyway).
To work around this, we could find the minimum existing value in the index using a single index seek. It would serve as a lower bound for the range. Since in real table that would most probably be something like 0 or 1, that would make the range much more constrained.
All these three methods could be used at the same time. Since the methods require nothing but just a single lookup of the statistics table and a single index seek, the most efficient method to return the subset of values that could satisfy the range could be chosen at runtime.
Implementation
Now, let's make a sample table in PostgreSQL and see how could we benefit from replacing the low-cardinality ranges with the lists of values:
This table contains 16,000,000 records with two integer fields and two double precision fields.
There are composite indexes on the pairs of fields. This indexes are intentionally created with the least selective column leading to demonstrate the benefits of range transformation.
First, let's run a query similar to the original one:
SELECT SUM(LENGTH(stuffing))
FROM t_composite
WHERE 1 = 1
AND uint1 <= 20
AND uint2 <= 20
| sum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 75600 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 row fetched in 0.0001s (5.1249s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aggregate (cost=171331.57..171331.58 rows=1 width=204)
-> Index Scan using ix_composite_uint on t_composite (cost=0.00..171329.57 rows=796 width=204)
Index Cond: ((uint1 <= 20) AND (uint2 <= 20))
The plan says that the index condition involves both fields. However, only the first field is used in the B-Tree search: the second is just being filtered on, though no actual table access is performed yet on this step.
The index keys are not too long, however, there are several millions of them that need to be scanned. That's why the query takes more than 5 seconds to complete.
The I/O statistics show the following:
SELECT pg_stat_reset();
SELECT SUM(LENGTH(stuffing))
FROM t_composite
WHERE 1 = 1
AND uint1 <= 20
AND uint2 <= 20;
SELECT pg_stat_get_blocks_fetched('ix_composite_uint'::regclass);
| pg_stat_get_blocks_fetched |
|---|
| 21865 |
The query required more than twenty thousands of index blocks to be read and examined
Smallest superset
Now, let's try to substitute the hard-coded list of possible values instead of the range condition:
SELECT SUM(LENGTH(stuffing)) FROM t_composite WHERE 1 = 1 AND uint1 IN ( SELECT generate_series(0, 20) ) AND uint2 <= 20
| sum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 75600 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 row fetched in 0.0001s (0.0063s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aggregate (cost=167.47..167.49 rows=1 width=204)
-> Nested Loop (cost=0.02..167.37 rows=40 width=204)
-> HashAggregate (cost=0.02..0.03 rows=1 width=4)
-> Result (cost=0.00..0.01 rows=1 width=0)
-> Index Scan using ix_composite_uint on t_composite (cost=0.00..166.84 rows=40 width=208)
Index Cond: ((t_composite.uint1 = (generate_series(0, 20))) AND (t_composite.uint2 <= 20))
Instead of a giant singe range, there are 21 short ranges examined in a nested loop. This is instant (6 ms).
Let's look into the I/O statistics again:
SELECT pg_stat_reset();
SELECT SUM(LENGTH(stuffing))
FROM t_composite
WHERE 1 = 1
AND uint1 IN
(
SELECT generate_series(0, 20)
)
AND uint2 <= 20;
SELECT pg_stat_get_blocks_fetched('ix_composite_uint'::regclass);
| pg_stat_get_blocks_fetched |
|---|
| 64 |
Now, only 64 blocks need to be read.
MIN / MAX
We took 0 as the initial value, but since theoretically there can be negative numbers in the columns, this assumption is not safe.
We need to get the least value from the table instead of assuming it:
SELECT SUM(LENGTH(stuffing)) FROM t_composite WHERE 1 = 1 AND uint1 IN ( SELECT generate_series( ( SELECT MIN(uint1) FROM t_composite ), 20) ) AND uint2 <= 20
| sum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 75600 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 row fetched in 0.0001s (0.0066s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aggregate (cost=171.40..171.41 rows=1 width=204)
-> Nested Loop (cost=3.95..171.29 rows=40 width=204)
-> HashAggregate (cost=3.95..3.96 rows=1 width=4)
-> Result (cost=3.92..3.93 rows=1 width=0)
InitPlan 2 (returns $1)
-> Result (cost=3.91..3.92 rows=1 width=0)
InitPlan 1 (returns $0)
-> Limit (cost=0.00..3.91 rows=1 width=4)
-> Index Scan using ix_composite_uint on t_composite (cost=0.00..62571556.68 rows=15999664 width=4)
Filter: (uint1 IS NOT NULL)
-> Index Scan using ix_composite_uint on t_composite (cost=0.00..166.84 rows=40 width=208)
Index Cond: (("20100519_cardinality".t_composite.uint1 = (generate_series($1, 20))) AND ("20100519_cardinality".t_composite.uint2 <= 20))
This is instant again.
Now, what about statistics?
SELECT pg_stat_reset();
SELECT SUM(LENGTH(stuffing))
FROM t_composite
WHERE 1 = 1
AND uint1 IN
(
SELECT generate_series(
(
SELECT MIN(uint1)
FROM t_composite
), 20)
)
AND uint2 <= 20;
SELECT pg_stat_get_blocks_fetched('ix_composite_uint'::regclass);
| pg_stat_get_blocks_fetched |
|---|
| 67 |
The query is only 3 block reads heavier, but this time it is guaranteed to be correct.
Loose index scan
The real* columns hold the double precision data.
First, let's run the original query:
SELECT SUM(LENGTH(stuffing))
FROM t_composite
WHERE 1 = 1
AND real1 <= 0.2
AND real2 <= 0.2
| sum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 83600 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 row fetched in 0.0001s (6.6561s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aggregate (cost=206210.82..206210.84 rows=1 width=204)
-> Index Scan using ix_composite_real on t_composite (cost=0.00..206208.84 rows=793 width=204)
Index Cond: ((real1 <= 0.2::double precision) AND (real2 <= 0.2::double precision))
Again, there are way too many block reads:
SELECT pg_stat_reset();
SELECT SUM(LENGTH(stuffing))
FROM t_composite
WHERE 1 = 1
AND real1 <= 0.2
AND real2 <= 0.2;
SELECT pg_stat_get_blocks_fetched('ix_composite_real'::regclass);
| pg_stat_get_blocks_fetched |
|---|
| 30657 |
, and the query takes more than 6 seconds.
For a condition like real1 <= 0.2, the smallest superset of all possible values (that is all possible double-precision values between 0 and 0.2) would be too large (though still finite of course) to be generated and joined. That's why we need to use server-collected statistics to decide whether a loose index scan would be efficient to get the list of all distinct values of real1 in the table:
SELECT n_distinct, most_common_vals, histogram_bounds
FROM pg_stats
WHERE schemaname = '20100519_cardinality'
AND tablename = 't_composite'
AND attname IN ('real1', 'real2')
| n_distinct | most_common_vals | histogram_bounds | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 40 | {0.09,0.22,0.01,0.37,0.04,0.25,0.28,0.34,0.27,0.06,0.36,0.11,0.08,0.39,0.12,0.2,0.02,0.16,0.17,0.21,0.29,0.18,0.19,0.26,0.3,0.32,0.35,0.1,0.13,0.4,0.15,0.23,0.38,0.03,0.33,0.24,0.07,0.14,0.05,0.31} | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 362181 | {1781.85,128.6,142.73,257.88,332.62,618.61,705.35,829.91,845.82,874.08,1432.82,1469.16,1486.01,1569.16,1866.43,2111.48,2234.48,2282.78,2340.7,2382.54,2468.19,2491.35,2494.73,2508.51,2587.51,2750.98,2876.07,2956.11,3222.62,3463.2,3564.41,3872.25,3.43,13.22,14.3,15.82,16.12,16.36,19.98,21.79,23.03,25.41,28.24,28.96,31.95,35.1,36.31,38.46,39.72,39.87,42.42,49.32,50.84,56.59,60.31,81.8,84.48,84.74,86.62,88.58,91.82,103.48,112.88,114.99,117.55,119.55,122.52,123.04,127.98,128.26,130.56,131.15,134.57,134.91,135.8,139.05,139.41,141.39,146.13,151.92,158.16,158.58,161.71,169.92,170.43,173.3,173.74,178.06,189.43,192.99,199.69,210.98,218.45,225.44,230.16,233.25,233.67,240.9,246.5,249.77} | {0.07,44.3,86.34,129.18,172.01,212.46,254.83,294.83,336.18,374.44,414.75,458.07,498.72,540.88,582.92,621.95,660.28,700.75,738.46,778.95,822.09,857.34,896.27,937.63,977.05,1017.49,1062.93,1104.88,1147.17,1185.99,1225.41,1267.8,1307.45,1347.49,1386.1,1424.05,1465.05,1503.23,1542.03,1581.45,1619.53,1658.57,1697.74,1741.65,1782.59,1823.19,1867.54,1905.59,1945.39,1986.04,2022.32,2061.52,2102.77,2143.07,2180.29,2218.06,2262.62,2302.28,2342.05,2382.29,2416.18,2455.43,2489.25,2528.07,2572.15,2606.91,2648.59,2685.43,2724.9,2765.49,2805.78,2845.94,2886.33,2925.52,2967.07,3005.12,3046.34,3084.44,3122.81,3158.25,3199.74,3242.4,3279.34,3319.41,3359.39,3401.15,3436.32,3477.28,3517.05,3559.6,3599.6,3639.63,3678.82,3720.27,3760.32,3801.89,3844.98,3883.96,3922.63,3963.01,3999.98} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 rows fetched in 0.0003s (0.0072s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
From the server statistics we see that there are only 40 distinct values of real1. Hence, a loose index scan as such would be efficient.
Let's look into the stats on real2. We see that there are 362181 distinct values in the table, and the range in question (<= 0.2) corresponds to the first entry in the histogram (BETWEEN 0.07 AND 44.3). Since the histogram splits the values into 100 percentiles, this means that there are about 3622 values from 0.07 to 44.3, and ((0.2 - 0.07) / (44.3 - 0.07) * 362181 / 100) ≈ 11 distinct values inside our range, and about 11 * 16000000 /362181 ≈ 486 records with these values.
Taking into account that the original query would need to scan 8,000,000 records, the loose index scan seems to be a good idea.
Unfortunately, PostgreSQL does not support it directly, but with minimal effort it can be emulated:
WITH RECURSIVE q (real1) AS
(
SELECT MIN(real1)
FROM t_composite
UNION ALL
SELECT (
SELECT c.real1
FROM t_composite c
WHERE c.real1 > q.real1
AND c.real1 <= 0.2
ORDER BY
c.real1
LIMIT 1
)
FROM q
WHERE q.real1 IS NOT NULL
)
SELECT SUM(LENGTH(stuffing))
FROM q
JOIN t_composite c
ON c.real1 = q.real1
AND c.real2 <= 0.2
| sum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 83600 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 row fetched in 0.0001s (0.0082s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aggregate (cost=17319.78..17319.80 rows=1 width=204)
CTE q
-> Recursive Union (cost=3.92..401.33 rows=101 width=8)
-> Result (cost=3.92..3.93 rows=1 width=0)
InitPlan 1 (returns $1)
-> Limit (cost=0.00..3.92 rows=1 width=8)
-> Index Scan using ix_composite_real on t_composite (cost=0.00..62694798.76 rows=15999664 width=8)
Filter: (real1 IS NOT NULL)
-> WorkTable Scan on q (cost=0.00..39.54 rows=10 width=8)
Filter: (q.real1 IS NOT NULL)
SubPlan 2
-> Limit (cost=0.00..3.93 rows=1 width=8)
-> Index Scan using ix_composite_real on t_composite c (cost=0.00..314695.34 rows=79998 width=8)
Index Cond: ((real1 > $2) AND (real1 <= 0.2::double precision))
-> Nested Loop (cost=0.00..16914.48 rows=1588 width=204)
-> CTE Scan on q (cost=0.00..2.02 rows=101 width=8)
-> Index Scan using ix_composite_real on t_composite c (cost=0.00..166.95 rows=40 width=212)
Index Cond: ((c.real1 = q.real1) AND (c.real2 <= 0.2::double precision))
This is almost instant again. Here are the I/O statistics:
SELECT pg_stat_reset();
WITH RECURSIVE q (real1) AS
(
SELECT MIN(real1)
FROM t_composite
UNION ALL
SELECT (
SELECT c.real1
FROM t_composite c
WHERE c.real1 > q.real1
AND c.real1 <= 0.2
ORDER BY
c.real1
LIMIT 1
)
FROM q
WHERE q.real1 IS NOT NULL
)
SELECT SUM(LENGTH(stuffing))
FROM q
JOIN t_composite c
ON c.real1 = q.real1
AND c.real2 <= 0.2;
SELECT pg_stat_get_blocks_fetched('ix_composite_real'::regclass);
| pg_stat_get_blocks_fetched |
|---|
| 165 |
The number of index reads is reduced greatly again.
Summary
In some cases, a range predicate (like less than
, greater than
or between
) can be rewritten as an IN predicate against the list of values that could satisfy the range condition.
Depending on the column datatype, check constraints and statistics, that list could be comprised of all possible values defined by the column's domain; all possible values defined by column's minimal and maximal value, or all actual distinct values contained in the table. In the latter case, a loose index scan could be used to retrieve the list of such values.
Since an equality condition is applied to each value in the list, more access and join methods could be used to build the query plain, including range conditions on secondary index columns, hash lookups etc.
Whenever the optimizer builds a plan for a query that contains a range predicate, it should consider rewriting the range condition as an IN predicate and use the latter method if it proves more efficient.
 Subscribe in a reader
Subscribe in a reader
great article :)
Thanks
marc-o
23 May 10 at 23:00
Great article, and I think it provides an answer to a stackoverflow question. I posted an answer with a link to this article and I included your summary in the answer. I hope this is ok. The link to the answer is:
http://stackoverflow.com/questions/2914082/how-do-you-design-a-database-to-allow-fast-multicolumn-searching/2915541#2915541
Trey Jackson
26 May 10 at 22:08
@Trey: the mechanism used for a multi-column search with ranged conditions would be similar indeed. The article actually discusses the mechanism’s integration into the query optimizers: an experienced developer can rewrite the query using the same approach I used in the article. The query still needs to be backed by a composite index (or a number of indexes) on the appropriate columns, though.
Quassnoi
27 May 10 at 02:05
Nice article, as always. Big fan of your site, thanks!
Frode
18 Jun 10 at 15:48
@Frode: thanks!
Quassnoi
22 Jun 10 at 11:15
Thanks for letting us understand how indexing works, I did understood well now.
Thanks for the good work.
Just curious to know how does these number works with “joins” (many-tables).
Rakesh
2 Jul 10 at 11:35
@author/admin:-
If you guys have a plugin which will give you the list of related articles in end of each blog sections will be great.
Rakesh
2 Jul 10 at 11:37
@Quassnoi thank you for a deeply thought-provoking article. I personally find it shocking that a RDBMS cannot efficiently process ranges, as you have proven. I thought that < 20 would have done exactly what IN () is doing. To me, it seems obvious that is should. Does SQL Server suffer this fate too?
On a related point, if those columns were individually indexed, as opposed to indexed as you have done with low cardinality, would we still be looking at the scenario you outline here?
Ian
14 Nov 10 at 01:14
@Ian:
I thought that < 20 would have done exactly what IN () is doing
IN()on what column type?If the column type is, say,
FLOAT, the smallest superset of the values that satisfy the condition is close to infinity (I know this is wrong in math sense, but you know what I mean). It’s infeasible to convert the range into the set.If the type is
UNSIGNED INTthen of course it can and sometimes needs to be done.No optimizer known to me is able to do it, if that was your question, that’s why I wrote this article.
On a related point, if those columns were individually indexed, as opposed to indexed as you have done with low cardinality, would we still be looking at the scenario you outline here?
The optimizers are capable of doing
INDEX_INTERSECT, that is selecting the recordsets satisfying each condition separately then joining these recordsets. This would require scanning 20000 + 20000 = 40000 records plus overhead of joining them, as opposed to just 400 records with a range rewrite.Quassnoi
14 Nov 10 at 16:28
@Quassnoi thanks for your reply. I mean IN() on int types. Ok, something here seems illogical to me (not from you). Taking your example, let’s look at the quantity column. If it is indexed, then we know it’s sorted. So if we query “<= 4", then surely the query engine will walk only the top of the index until it finds 5, at which point it will quit, having found all the records that satisfy "<= 4". Then it would either do a table scan **only on the relevant records** to filter urgency, OR, better, it would do a walk-through on the urgency index, find all records for "<= 4", and then perform an index intersect on the two index result sets, giving us the RIDs we're looking for. To me, this is logical. I don't see why it needs to scan 40k records.
Ian
14 Nov 10 at 18:18
So if we query “<= 4″, then surely the query engine will walk only the top of the index until it finds 5, at which point it will quit, having found all the records that satisfy “<= 4”
That’s 5000 records (from 1 to 5000)
Then it would either do a table scan **only on the relevant records** to filter urgency,
Urgencyis not a part of the index onquantity. We’ll have to do a table lookup for each of 5000 records, each of them being about five times as costly.Better, it would do a walk-through on the urgency index, find all records for “<= 4”, and then perform an index intersect on the two index result sets, giving us the RIDs we’re looking for
That’s another 5000 records, plus the overhead of a join between the resultsets — opposed to 25 (twenty five) index seeks in a composite index with an
INrewrite.I don’t see why it needs to scan 40k records.
If we substitute 5 with 20 (as in your original comment), we’ll get 40k vs 400. If we leave 5 as is, we’ll get 10k vs 25.
Quassnoi
14 Nov 10 at 19:13
“That’s 5000 records (from 1 to 5000)”
“That’s another 5000 records”
I’m missing why it would need to do any record look-ups when all the data is contained in 2 indexes. Table lookups would only happen once the RIDs had been calculated via index lookup ops.
Ian
14 Nov 10 at 19:45
I’m missing why it would need to do any record look-ups when all the data is contained in 2 indexes
Each index, as you suggested them, contains data on the respective field only (one on
quantity, another one onurgency). There is no information abouturgencyin thequantityindex and vice versa. You should look that up in the table.Of course you could make both indexes covering, but this would still require you to scan 5k records (instead of but 25).
Quassnoi
14 Nov 10 at 20:34
This article seems to be attempting a similar goal, but in a different way. http://wiki.postgresql.org/wiki/Loose_indexscan
Ian
2 Jan 11 at 11:48
As a math major you is not going to only be taught a whole lot of mathematics,
but you’ll strengthen your drawback-solving skills, sharpen your crucial considering abilities,
and be higher prepared for all times after college https://math-problem-solver.com/ .
I’d say that this could individuals of varying talents.
Ula Close
5 Feb 18 at 22:56