Things SQL needs: MERGE JOIN that would seek
One of the most known and least used join algorithms in SQL engines is MERGE JOIN.
This algorithm operates on two sorted recordsets, keeping two pointers that chase each other.
The Wikipedia entry above describes it quite well in terms of algorithms. I'll just make an animated GIF to make it more clear:
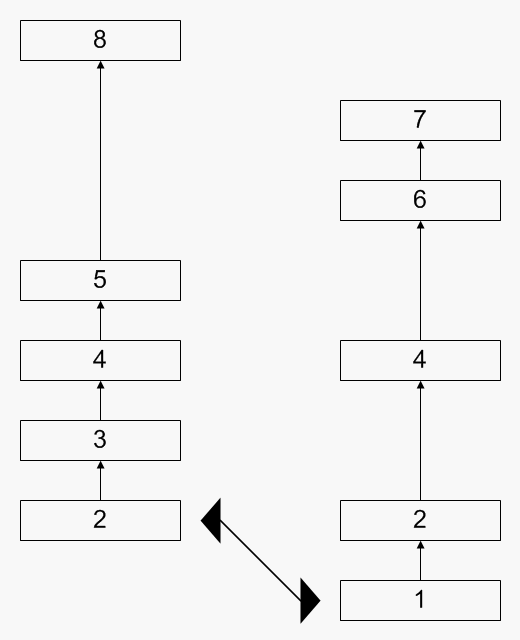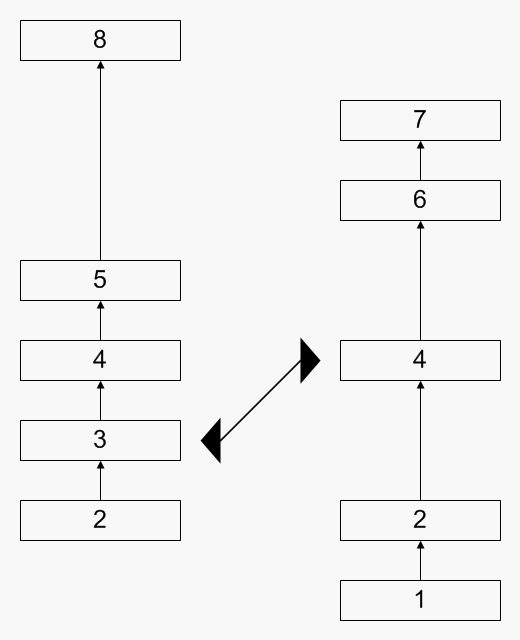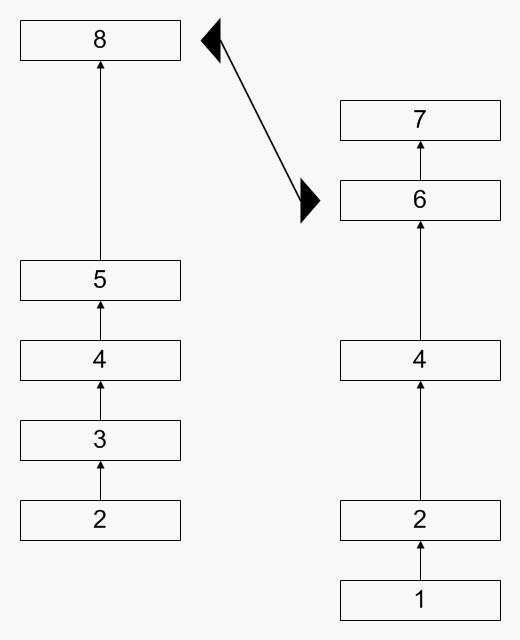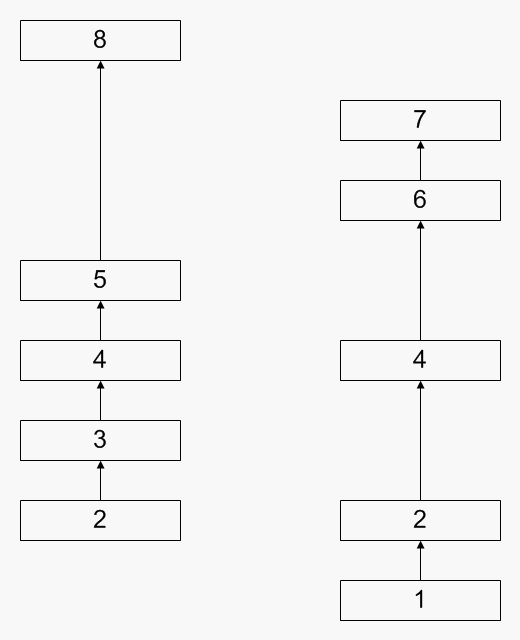
This is quite a nice and elegant algorithm, which, unfortunately, has two major drawbacks:
- It needs the recordsets to be sorted
- Even with the recordsets sorted, it is no better than a
HASH JOIN
The sorting part is essential for this algorithm and there is nothing that can be done with it: the recordsets should be sorted, period. Databases, however, often provide the records in the sorted order: from clustered tables, indexes, previously sorted and ordered subqueries, spool tables etc.
But even when the recordsets are already sorted, on equijoins the MERGE JOIN is hardly faster than a HASH JOIN.
Why?
MERGE JOIN vs. HASH JOIN
Let's remember how the HASH JOIN works:
- It takes the smaller table and builds a hash table out of it, with the join key as the hash key.
- Then it takes each record from the larger table and looks it up in the hash table. If found, the records are returned.
We see that there are four major steps involved:
- Scan the smaller table
- Build a hash table (i. e. copy each record from the smaller table into the hash slot)
- Scan the larger table
- Look up the larger table
Since building and looking up the hash table are performed in memory (or, depending on the SQL engine implementation, in memory-mapped temporary database, which is almost the same), these steps take negligible time compared to the time required to scan the table.
But we see that MERGE JOIN, as it is implemented now, also requires scanning both recordsets. Each record should be evaluated by the pointer to figure out if its join key is more, less or equal to that of the the other pointer.
This means that both MERGE JOIN and HASH JOIN require scanning both recordsets. However, HASH JOIN does not require any special order, which means it can use a table scan, index fast full scan and any other methods to get the records all at once, while MERGE JOIN need either to sort the records (which is obviously slow) or to traverse the index with the subsequent key lookups (which is not fast too).
In some terminal cases MERGE JOIN can be more efficient indeed: say, when the hash table does not fit completely into memory and would require either extensive disk writes or several scans over the source tables, while a MERGE JOIN could be performed on a pair of indexes.
It is also efficient for FULL OUTER JOIN: each record is evaluated, returned and forgotten only once, while HASH JOIN would require a second pass over the records that had not been ever matched.
Seeks instead of scans
But does the MERGE JOIN really always need to traverse all records?
Let's see some more pictures:
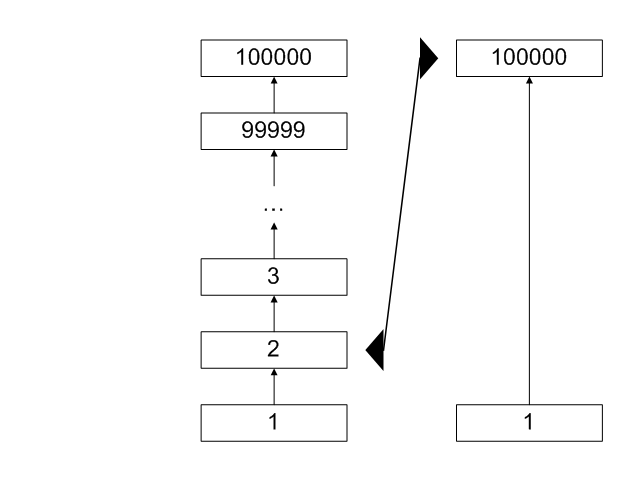
Here, the right recordset is 100,000 records ahead of the left recordset. With MERGE JOIN, 100,000 records should be scanned from the left recordset and 100,000 comparisons made.
This is unavoidable if the recordset is a result of a sort operation.
However, MERGE JOIN is usually chosen when there is a more efficient sorted row source available: an index or a spool table (temporary index built in runtime). And both these sources allow efficient random seeks.
If an index served as the left recordset, we could see that right pointer is too far ahead, and just seek for its value in the left recordset instead of scanning 100,000 records:
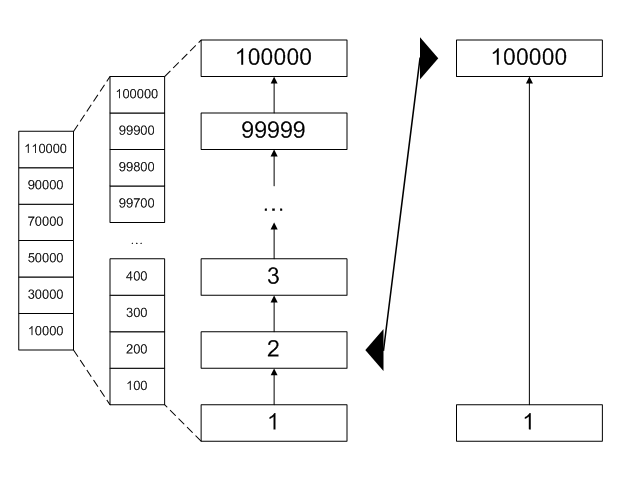
Here, we can see that 100,000 is too far away and could advance the left pointer to the position of the right pointer in only several reads, traversing the B-Tree.
Since the indexes usually collect statistics, all we would need to do to decide whether we need to seek or scan was to check the histograms to estimate how may records are there between the current and the opposite pointers. If there are too many, the seek cost would overweight the scan cost and a seek should be performed. The statistics table itself would not need to be queried too often: since the records are always selected in order, the statistics table could be also read sequentially.
Emulation
Let's create a couple of PostgreSQL tables and see the performance benefit:
These two tables have 1,000,000 records each, and a common column that would return only 1,000 records in a join.
Here's the plain query runs against these tables:
SELECT SUM(LENGTH(l.stuffing) + LENGTH(r.stuffing)) FROM t_left l JOIN t_right r ON r.bad = l.bad
| sum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 400000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 row fetched in 0.0001s (1.4062s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aggregate (cost=71338.33..71338.35 rows=1 width=408)
-> Merge Join (cost=58737.16..68838.33 rows=1000000 width=408)
Merge Cond: (l.bad = r.bad)
-> Index Scan using ix_left_bad on t_left l (cost=0.00..56287.36 rows=1000000 width=208)
-> Index Scan using ix_right_bad on t_right r (cost=0.00..56287.36 rows=1000000 width=208)
Note that PostgreSQL used a MERGE JOIN without any tricks from our side. This is because the table records are too large and could not fit into a hash table all at once.
Of course, PostgreSQL could only store the record pointers in the hash table and do the record lookups after the join, however, for some reason it would not select this plan.
MERGE JOIN, in our case, is quite efficient, since the indexes are read first and the actual records are only looked up for the matched records (which are not too numerous). However, it still requires traversing 2,000,000 records which takes more than a second.
Now, let's emulate the MERGE JOIN doing the seeks instead of scans. To do that, we will write a recursive query:
WITH RECURSIVE q (l, r) AS
(
SELECT (
SELECT l
FROM t_left l
ORDER BY
bad
LIMIT 1
),
(
SELECT r
FROM t_right r
ORDER BY
bad
LIMIT 1
)
UNION ALL
SELECT CASE
WHEN (q.l).bad < (q.r).bad THEN
(
SELECT li
FROM t_left li
WHERE li.bad >= (q.r).bad
ORDER BY
bad
LIMIT 1
)
WHEN (q.l).bad = (q.r).bad THEN
(
SELECT li
FROM t_left li
WHERE li.bad > (q.r).bad
ORDER BY
bad
LIMIT 1
)
ELSE
l
END,
CASE
WHEN (q.r).bad < (q.l).bad THEN
(
SELECT ri
FROM t_right ri
WHERE ri.bad >= (q.l).bad
ORDER BY
bad
LIMIT 1
)
WHEN (q.r).bad = (q.l).bad THEN
(
SELECT ri
FROM t_right ri
WHERE ri.bad > (q.l).bad
ORDER BY
bad
LIMIT 1
)
ELSE
r
END
FROM q
WHERE l IS NOT NULL
AND r IS NOT NULL
)
SELECT SUM(LENGTH((q.l).stuffing) + LENGTH((q.r).stuffing))
FROM q
WHERE (q.l).bad = (q.r).bad
| sum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 400000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 row fetched in 0.0001s (0.0481s) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aggregate (cost=30.94..30.96 rows=1 width=64)
CTE q
-> Recursive Union (cost=0.11..28.66 rows=101 width=64)
-> Result (cost=0.11..0.12 rows=1 width=0)
InitPlan 1 (returns $1)
-> Limit (cost=0.00..0.06 rows=1 width=36)
-> Index Scan using ix_left_bad on t_left l (cost=0.00..56287.36 rows=1000000 width=36)
InitPlan 2 (returns $2)
-> Limit (cost=0.00..0.06 rows=1 width=36)
-> Index Scan using ix_right_bad on t_right r (cost=0.00..56287.36 rows=1000000 width=36)
-> WorkTable Scan on q (cost=0.00..2.65 rows=10 width=64)
Filter: ((q.l IS NOT NULL) AND (q.r IS NOT NULL))
SubPlan 3
-> Limit (cost=0.00..0.06 rows=1 width=36)
-> Index Scan using ix_left_bad on t_left li (cost=0.00..19598.69 rows=333333 width=36)
Index Cond: (bad >= ($3).bad)
SubPlan 4
-> Limit (cost=0.00..0.06 rows=1 width=36)
-> Index Scan using ix_left_bad on t_left li (cost=0.00..19598.69 rows=333333 width=36)
Index Cond: (bad > ($3).bad)
SubPlan 5
-> Limit (cost=0.00..0.06 rows=1 width=36)
-> Index Scan using ix_right_bad on t_right ri (cost=0.00..19598.69 rows=333333 width=36)
Index Cond: (bad >= ($4).bad)
SubPlan 6
-> Limit (cost=0.00..0.06 rows=1 width=36)
-> Index Scan using ix_right_bad on t_right ri (cost=0.00..19598.69 rows=333333 width=36)
Index Cond: (bad > ($4).bad)
-> CTE Scan on q (cost=0.00..2.27 rows=1 width=64)
Filter: ((l).bad = (r).bad)
This query makes a seek each time it needs to advance a pointer. This is not the most efficient way, but despite that fact, this query completes in only 40 ms, which is 25 times as fast as the plain MERGE JOIN query.
Summary
With its current implementation, MERGE JOIN is not the most efficient algorithm, however, for several types of queries it outperforms HASH JOIN.
The main drawback of the MERGE JOIN is its inability to use seeks to advance the record pointers. Even if the opposite pointer is far away, the sequential scan is used instead of a B-Tree seek, even if the recordset is an index or a spool table.
To improve this, the accumulated index statistics should be taken into account when deciding whether to perform a seek or a sequential scan to catch up with the opposite pointer. If the statistics show a high number of the records in between, an index seek should be used instead of the index scan.
With this improvement, MERGE JOIN would perform much better, especially when joining two large indexed tables. It would require much less resources than a HASH JOIN, and, unlike NESTED LOOPS, the seeks would be performed only when really needed, thus preserving the benefits of the sequential access to the tables.
 Subscribe in a reader
Subscribe in a reader
Amazingly insightful and well-written :)
Kudos – your articles are always a pleasure to read.
regards,
Roland
Roland Bouman
9 May 10 at 01:31
@Roland: thanks!
Quassnoi
9 May 10 at 02:28
Well-written..
Cihan Demir
9 May 10 at 17:28
This is great! I ran into this today when I (incorrectly) figured that a merge join would be faster and experimented with forcing it into my execution plan. When to my surprise it switched from a seek to a scan, I had to figure out why. Now I understand! I had the same reaction you did: why can’t it seek when it makes sense to?
Thanks for explaining.
Emtucifor
14 Sep 10 at 23:29
@Emtucifor: my pleasure!
Quassnoi
14 Sep 10 at 23:37
It helps very much to understand about Merge join and Hash Join.
chandrashekhar singh
10 Dec 10 at 00:05
Thank you.
I’ve watched your blog posts for 3 years. Best resource ever.
iapilgrim
17 Sep 14 at 07:14